1 引言

分形天線是分形幾何與天線工程相結(jié)合的產(chǎn)物，它具有小型化、多頻帶、可集成等優(yōu)良特性，是當(dāng)前天線工程中一個新的研究熱點(diǎn)[1][2]。

分形天線的幾何形狀具有自相似性，即局部與整體、局部與局部之間具有相似的形狀。Sierpinski三角形是一種具有自相似性的幾何圖形，用這種幾何形狀取代常規(guī)的圓柱狀來作為天線的振子，使得天線具有多頻帶特性。

2 Sierpinski三角形的形成過程

Sierpinski三角形是從一個正三角形中反復(fù)依次去掉一個反向的正三角形構(gòu)造出來的，如圖1所示。在幾何構(gòu)圖中，Sierpinski三角形的形成是一種迭代過程。在一次迭代中，產(chǎn)生Sierpinski三角形的迭代函數(shù)系統(tǒng)包含三個仿射變換。三個變換所產(chǎn)生的復(fù)制圖，其大小均為原圖的一半，其位置成120°分別向三個方向移動原三角形高的1/3。按照這樣的迭代函數(shù)進(jìn)行無數(shù)次迭代，便可以形成具有分形結(jié)構(gòu)的Sierpinski三角形。顯然，這種結(jié)構(gòu)具有自相似性。

3 Sierpinski單極子天線的性能分析

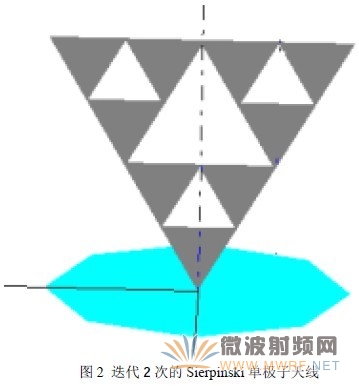
用Sierpinski三角形代替常規(guī)的圓柱狀振子，可以構(gòu)成Sierpinski單極子天線（如圖2所示）和Sierpinski偶極天線。 利用Ansoft公司的HFSS軟件，分別計算了迭代0次、迭代1次、迭代2次的Sierpinski單極子天線的反射損耗特性（如圖3所示）。所計算天線的反射面直徑為800mm，高為800mm。在計算中，為了減小計算量，反射面采用正八邊形。

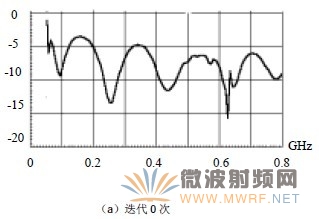
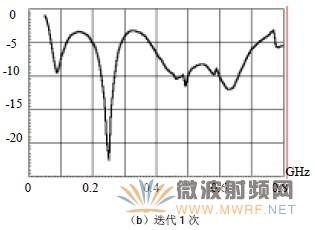
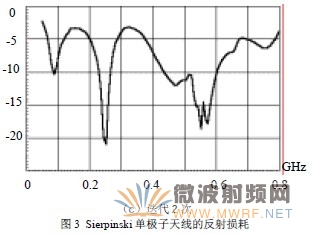
迭代0次的Sierpinski單極子天線實際上是三角形天線，本身具有較寬的頻率特性，但沒有明顯的諧振特性。比較圖3-b與圖3-a可以看出，迭代1次的Sierpinski單極子天線具有兩個明顯的諧振點(diǎn)，分別為85MHz和243MHz，而從圖3-c可以看出迭代2次的Sierpinski單極子天線具有三個明顯的諧振點(diǎn)，分別為85MHz、243MHz和575MHz。

上述Sierpinski單極子天線迭代的比例系數(shù)系數(shù)為0.5，因而其諧振頻率的比值應(yīng)為2。但是由于對于這種單極形式的Sierpinski天線，不是理想的分形結(jié)構(gòu)，所以只是接近2。諧振頻率在低端的差別更大，其原因是對于低端，反射面的相對電尺寸較小，只有1/2波長左右，這樣反射面的尺寸對于不同的諧振頻率的作用不完全相同。在高端，其電尺寸較大，對于不同的諧振頻率，反射面的作用基本相同，因而諧振頻率之比約為2。另外在實際應(yīng)用中，Sierpinski三角形的迭代次數(shù)只能是有限次，因而它不可能是理想的分形結(jié)構(gòu)，所以其諧振頻率之比不會嚴(yán)格等于2。

實際制作了迭代2次的Sierpinski單極子天線，其實測的結(jié)果如圖4所示。圖4的實測結(jié)果與圖3-c的計算結(jié)果比較相近，驗證了HFSS計算天線問題的正確性。

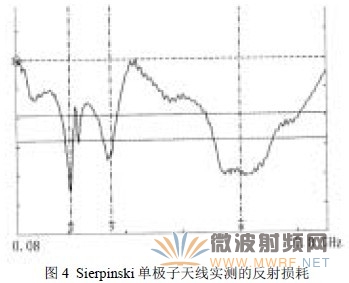
4 Sierpinski單極子天線的多頻帶設(shè)計

給定所需要的幾個頻段，如何設(shè)計出滿足要求的Sierpinski單極子天線是一個實際工程問題。在前面所述的Sierpinski三角形的形成過程中，原形是正三角形，迭代的比例系數(shù)系數(shù)為0.5。而實際上在天線的設(shè)計中，原形可以是等腰三角形或任意形狀的三角形，比例系數(shù)可以是0與1之間的任意數(shù)值。這樣就可以根據(jù)某些給定的頻段，進(jìn)行靈活設(shè)計。在設(shè)計過程中，為 2 使所設(shè)計的天線滿足所需要的頻段要求，可以利用HFSS軟件對設(shè)計參數(shù)進(jìn)行調(diào)整，這樣會很快得到所需要的設(shè)計參數(shù)，既省時省力，又節(jié)約成本，從而大大提高了天線設(shè)計工作的效率。

參考文獻(xiàn)：

[1] 田鐵紅，周正.分形天線的應(yīng)用研究[J]. 無線電工程，33（3）：16~20.
[2] 劉英，龔書喜，傅德民. 用于多頻通信的微帶分形貼片天線[J]. 微波學(xué)報， 17（4）：76~79.
[3] C.Puente-Baliarda，et al.，On the Behavior of the Sierpinski and Fractal Antenna[J]. IEEE Transations on Antenna and Propagation，1998，46（4）：517~524.
[4] C.Puente.etc. Fractal Multiband Antenna Based on the Sierpinski Gasket[J]. IEE Electronics Letters, 1996，32（1）：1~2.
[5] 胡瑞安，胡紀(jì)陽，徐樹公. 分形的計算機(jī)圖象及其應(yīng)用[M]. 中國鐵道出版社，1995.

作者：路志勇 董曉娟