一、引言

天線工程一問世，天線測(cè)量就是人們一直關(guān)注的重要課題之一，方法的精確與否直接關(guān)系到與之配套系統(tǒng)的實(shí)用與否。隨著通訊設(shè)備不斷更新，對(duì)天線的要求愈來愈高，常規(guī)遠(yuǎn)場(chǎng)測(cè)量天線的方法由于實(shí)施中存在著許多困難，有時(shí)甚至無能為力，于是人們就渴望通過測(cè)量天線的源場(chǎng)而計(jì)算出其輻射場(chǎng)的方法。然而由于探頭不夠理想和計(jì)算公式的過多近似，致使這種方法未能賦于實(shí)用。為了減小探頭與被測(cè)天線間的相互影響，Barrett等人在50年代采用了離開天線口面幾個(gè)波長(zhǎng)來測(cè)量其波前的幅相特性，實(shí)驗(yàn)結(jié)果令人大為振奮，由此掀開了近場(chǎng)測(cè)量研究的序幕，這一技術(shù)的出現(xiàn)，解決了天線工程急待解決而未能解決的許多問題，從而使天線測(cè)量手段以新的面目出現(xiàn)在世人的面前。

四十多年過去了，近場(chǎng)測(cè)量技術(shù)已由理論研究進(jìn)入了應(yīng)用研究階段，并由頻域延拓到了時(shí)域，它不僅能夠測(cè)量天線的輻射特性，而且能夠診斷天線口徑分布，為設(shè)計(jì)提供可靠、準(zhǔn)確設(shè)計(jì)依據(jù)；與此同時(shí)，人們利用它進(jìn)行了目標(biāo)散射特性的研究，即隱身技術(shù)和反隱身技術(shù)的研究，從而使該技術(shù)的研究有了新的研究手段，進(jìn)而使此項(xiàng)研究進(jìn)入了用近場(chǎng)測(cè)量的方法對(duì)目標(biāo)成像技術(shù)的探索階段。

二、近場(chǎng)測(cè)量技術(shù)發(fā)展的過程

近場(chǎng)測(cè)量的技術(shù)研究從五十年代發(fā)展至今，其研究方向大致經(jīng)歷四個(gè)階段，如表1所示。

表1 近場(chǎng)測(cè)量技術(shù)所經(jīng)歷的時(shí)間

1、理論研究

在Barrett等人的實(shí)驗(yàn)之后，Richnlond等人用空氣和介質(zhì)填充的開口波導(dǎo)分別測(cè)量了微波天線的近場(chǎng)，并把由近場(chǎng)測(cè)量所計(jì)算得到的方向圖與直接遠(yuǎn)場(chǎng)法測(cè)得的結(jié)果相比較，其方向圖在主瓣和第一副瓣吻合較好，遠(yuǎn)副瓣和遠(yuǎn)場(chǎng)法相差較大。于是人們就分析其原因，最終歸結(jié)為探頭是非理想起點(diǎn)源所致，因此，出現(xiàn)了各種方法的探頭修正理論。直到1963年Karns等人提出了平面波分析理論才從理論上嚴(yán)格地解決了非點(diǎn)源探頭修正的問題。與此同時(shí)，Paris和Leach等人用羅侖茲互易定理也推出了含有探頭修正的平面波與柱面波展開表達(dá)式^[1，2]。Joy等人也給出了含有探頭修正下的球面波展開式及其應(yīng)用^[3]。至此，頻域近場(chǎng)測(cè)量模式展開理論已完全成熟，因此研究者的目光投向了應(yīng)用領(lǐng)域。在隨后的十年里，美國(guó)標(biāo)準(zhǔn)局(NBS)等研究機(jī)構(gòu)進(jìn)行大量的實(shí)驗(yàn)證明此方法的準(zhǔn)確性^[4]，其中取樣間隔、探頭型式的選擇以及誤差分析是研究者們關(guān)心的熱門問題。

2、取樣間隔及取樣間距

由于模式展開理論是建立在付里葉變換的基礎(chǔ)上，根據(jù)付里葉變換中抽樣定理^[5]，對(duì)帶寬有限的函數(shù)。用求和代替積分，用增量代替積分元不引人計(jì)算誤差，而平面、柱面、球面的模式展開式對(duì)輻射場(chǎng)而言都是帶寬有限的函數(shù)，忽略探頭與被測(cè)天線間的電抗耦合(取樣間距選取的準(zhǔn)則)，取樣間隔與取樣間距按表2所示的準(zhǔn)則進(jìn)行選取(參看圖1坐標(biāo)系)。

表2 取樣間隔與取樣問距的準(zhǔn)則

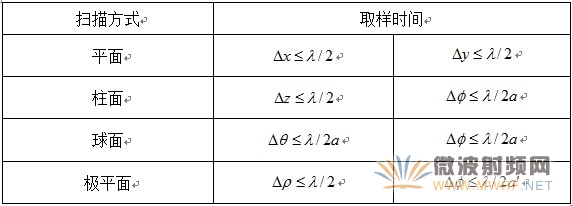
表中：λ —工作波長(zhǎng)；d—探頭距被測(cè)天線口徑面的距離；α—完全包圍教測(cè)天線最小柱面或球面的半徑；α'—極平面取樣的最大圓半徑．

如果d變小，則取樣間隔可按下式計(jì)算[6]

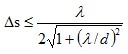(1)

若d≤λ/2，則取樣間距應(yīng)取為小于λ/4，這時(shí)可用有限頻譜法[7]修正感應(yīng)場(chǎng)對(duì)測(cè)量數(shù)據(jù)的影響。

取樣面尺寸與被測(cè)天線的口徑面大小有關(guān)。對(duì)于一維平面掃描的情況，取樣面的尺寸Lx與口徑面尺寸D有如下關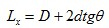(guān)系，參看圖2。

(2)

只要d選定，θ可由測(cè)量精度求得^[5]，則Lx是確定的。通常工程上要求和幅度方向圖副瓣電平測(cè)量誤差≤0.5dB，在此條件下，取樣面的尺寸可按下式選取(d≥λ)

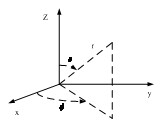
圖1 表2所用的坐標(biāo)系

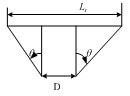
圖2一維平面掃描取樣面與被測(cè)天線口面尺寸的幾何關(guān)系

L_x=2X|_E=-40dB (3)

式中，X|_E=-40dB為低于取樣面中心場(chǎng)強(qiáng)40dB處的位置坐標(biāo)，其它情況依次類推。