我們在之前的博客中已經介紹了怎么利用對稱、反對稱，以及周期性邊界條件來節省電磁模型的建模時間。今天，我們將為您展示一個利用軸對稱建立的模型 — 錐型喇叭天線模型。

利用二維軸對稱節省建模時間

盡管我們能夠建立并求解三維的錐型喇叭天線模型，但是這類模型需要調用大量的計算資源來進行求解。利用結構的對稱性，我們可以非常快速地求解電磁場問題。因為我們處理的幾何是一個圓錐，模型在結構上關于軸對稱，所以可以采用二維軸對稱來簡化建模。

盡管結構上軸對稱，但是電磁場在繞軸的方位角上會有一些不同，所以電磁場具有方位角變量。RF模塊和波動光學模塊可以用來對于具有不同方位角模式數的軸對稱結構進行建模。

我們可以利用上述功能；通過創建一個二維軸對稱模型，求解多個不同的方位角模式數，從而可以創建一個相比完整三維模型的計算速度要快，但內存占用要少的模型。

喇叭天線的一般注意事項

喇叭天線可以根據整體造型以及內部構造分為各種樣式。這些屬性決定了天線的波束輪廓，帶寬以及交叉極化。

交叉極化是指電磁場的極化方向與期望的方向相反。例如，我們想要電磁場在垂直方向極化，結果卻在水平方向極化。

天線的漏斗狀部分與波導相連，將電磁波傳遞給天線。喇叭的形狀將決定其適用于什么應用。例如，扇形喇叭（下圖b 和c）的典型應用是全搜索雷達天線。

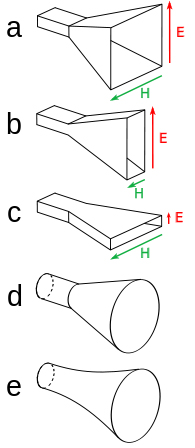
各種喇叭天線的形狀：a) 金字塔型；b) 扇形，E-面；c) 扇形，H-面；d) 圓錐形；e) 指數型。 “喇叭天線類型” 圖片為Chetvorno 制作，已獲得Creative Commons Zero 授權，并通過Wikimedia Commons分享。

波紋狀錐型喇叭天線模型

在我們例子中的天線形狀為錐型（如上圖d），天線內部的表面具有波紋；波紋狀錐型喇叭天線通過波導饋給。波導傳遞TE 模式的電磁波通過波紋漏斗，結果產生TM 模式的電磁波。由于在整個圓錐中都有波紋表面，所以不同的模式被混合在一起，相比于最初的激勵TE模式，孔隙處交叉極化更低。

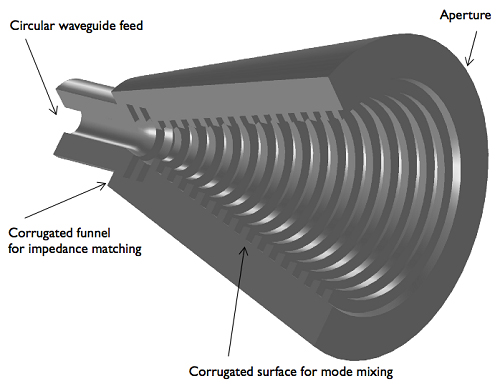
基于二維軸對稱模型建立的三維幾何視圖

錐型喇叭天線：基于二維軸對稱模型建立的三維幾何視圖。波導以TE_1m 模式饋給天線(m = ±1), 當其通過天線的時候與TM_1m 模式混合。

前文提及了交叉極化，但是為什么我們要減少交叉極化的發生呢？如果有大量的交叉極化發生，而附近的其他信道具有交替的垂直和水平極化的話，那么我們的信號就可能與附近的其他信道相干擾。這不是我們想要的。

研究喇叭天線中的交叉極化

為了研究交叉極化，我們可以使用COMSOL Multiphysics 及其RF 模塊來建立模型。就如前面提到的，我們可以使用二維軸對稱模型代替三維模型，從而節省計算時間。我們使用電磁波，頻域接口來創建模型。

我們將跳過創建模型的步驟，而是直接來分析結果。如果您想要復現下圖的結果，可以從案例庫中下載模型文檔和MPH 文件。

首先，我們可以看到天線的定向波束圖是：

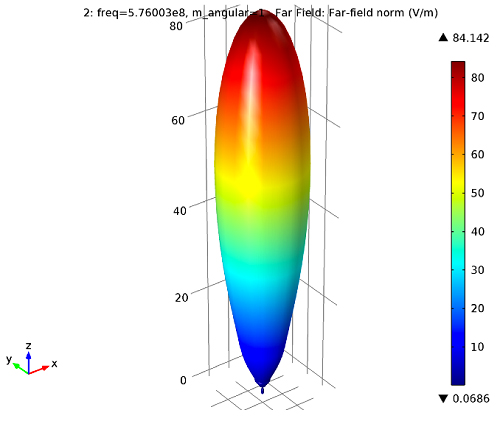
天線的定向波束圖的遠場圖

接下來，我們可以分析天線入口和出口處的電場。通過求解m = +1 和m = -1 時的模型，我們得以比較出口處x 和y 方向上的線性極化。

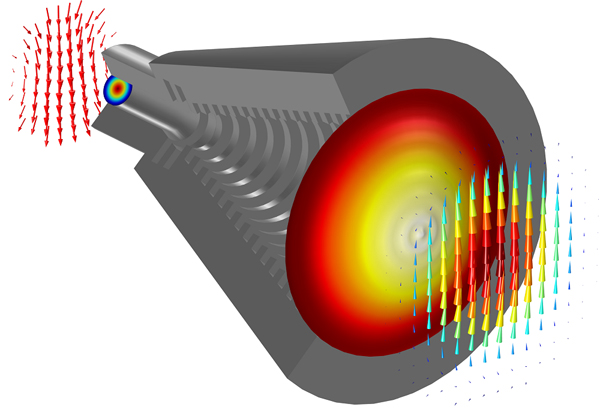
在天線入口和出口處的電場

m = +1和m = -1 的線性疊加，在天線入口和出口處的電場。

對于波導的饋給，場主要是沿x 方向，但不是線性極化。在孔隙處，場幾乎完全線性極化。為了量化兩個方向上的極化，我們可以計算錐型喇叭天線入口和出口位置各個電場分量絕對值的積分。計算之后我們得到，在入口處比例大約為5:1，而在出口處比例大概為40:1。換句話說，我們減少了8 倍的交叉極化。

來源：COMSOL博客

作者：Fanny Littmarck