學個Antenna是以天線仿真和調試為主，理論原理為輔的干貨天線技術專欄，包括天線入門知識以及各類天線的原理簡介、仿真軟件建模、設計、調試過程及思路。如有想看到的內容或技術問題，可以在文尾寫下留言。

摘要：

在淺談陣列天線及布陣一文中，我們知道了均勻直線陣的第一副瓣電平為－13.5dB。為了使雷達系統具有較高的抗干擾、抗反輻射導彈等的能力，現代電子戰對雷達天線提出了越來越低的副瓣要求。采用切比雪夫綜合法、泰勒綜合法等設計方法就可實現低副瓣。

本文使用的軟件為CST 2018和MATLAB R2019a

第一副瓣電平
在學個Antenna專欄的上次推文——淺談陣列天線及布陣，對均勻直線陣的陣因子進行了簡單的理論推導。歸一化陣因子為：

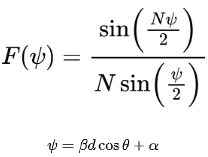
通過歸一化陣因子的表達式，可以求得其副瓣位置和副瓣電平值。要求得副瓣的位置，需要求得當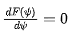時，的取值。

%matlab code clear;clc;N=10;format long; x=-pi/2:0.01:pi/2;y=abs(sin(N*x)./(N*sin(x))); %find first sidelobe [value1,id1]=findpeaks(y); [value2,id2]=sort(value1); first_sidelobe=20*log10(value2(end-1)); location=x(id1(floor(length(id1)/2))); plot(x,y,'r','linewidth',2); set(gca,'linewidth',3); xlabel('\psi','Fontsize',12); axis([-pi/2,pi/2,0,1]); h=legend({strcat('$$\left| {{{\sin \left( {N\psi} \right)} \over {N\sin \left( \psi \right)}}} \right|,N=',num2str(N),'$$'),...     },'interpreter','latex'); title({strcat('第一副瓣電平(dB)：',num2str(first_sidelobe));strcat('位置：',num2str(location))}); set(h,'FontName','Times New Roman','FontSize',12,'FontWeight','normal');

在MATLAB軟件跑上面的代碼，可以得到單元數N=10時，均勻直線陣等幅同相激勵下的陣因子圖。可能有人會疑問，均勻直線陣的第一副瓣電平不是-13.5dB么？差了0.5dB去哪了。

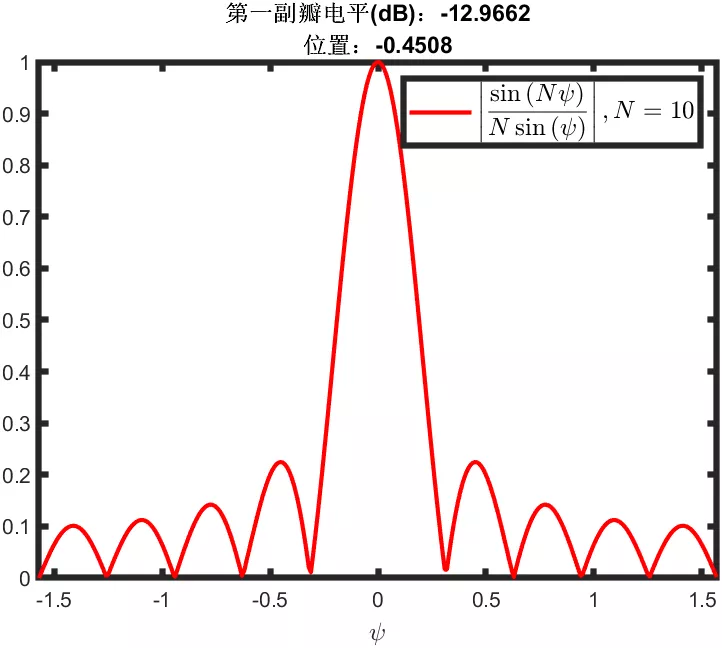
其實是單元數N取小了，將上面代碼的N賦值為50，將步進間隔由0.01改為0.0001，就會得到下圖，基本上達到了理論值。

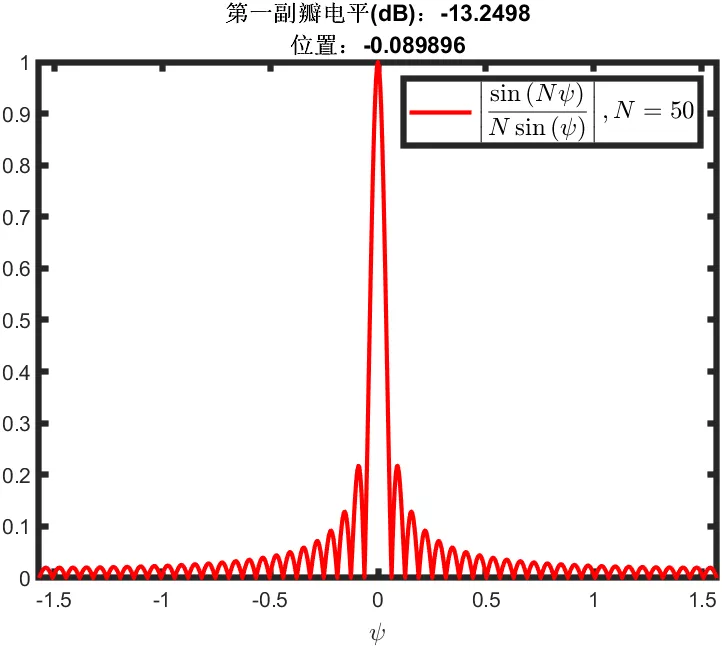
雖然與一般教材上的-13.5dB還有0.25dB差值，但這部分是因為這個函數求第一極值點采用了近似計算的方法，第一副瓣位置對應的位置值為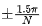。與實際副瓣位置點有一定的偏差造成的。

謝昆諾夫單位圓

對于一個等間距(d)排布饋電的N元直線陣，激勵電流幅度其陣因子為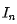，相鄰單元遞變相位差為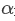，其線陣對應的陣因子為：

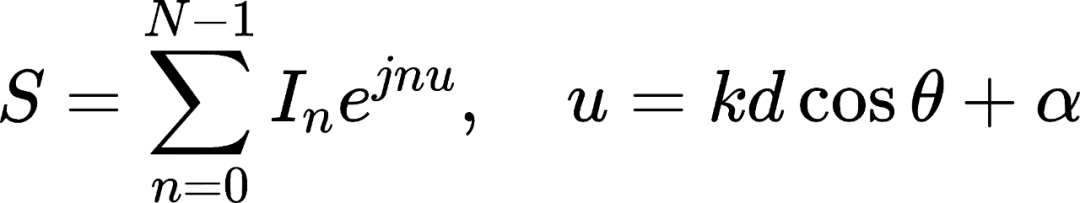
由于一個N-1次冪的多項式有N-1個復根，因此歸一化的上式可以寫成N-1個因式的連乘積形式：

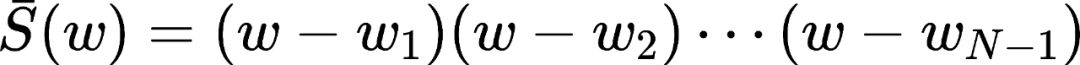
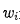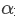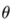式中，是多項式的根(零點)。自變量的相位與d、和有關。

自變量的軌跡是復平面內的一個圓，下圖為已知d和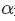時，w的軌跡隨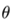變化：

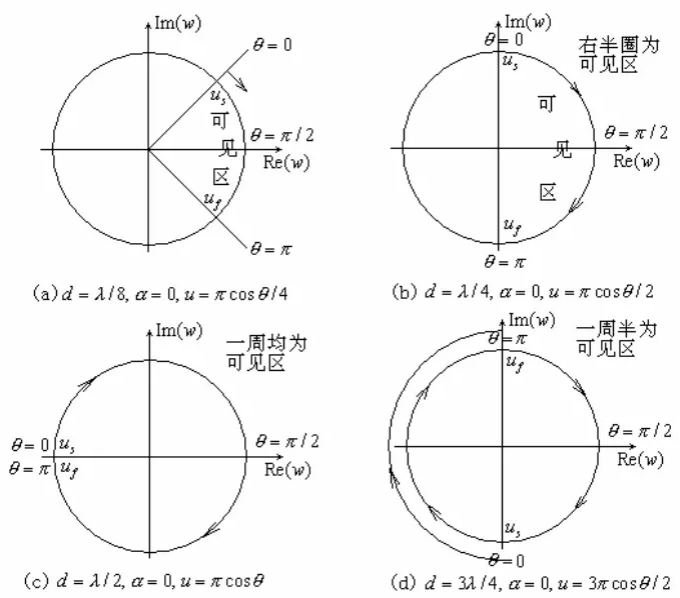
以五元等間距陣列為例，繪制除了四個零點在單位圓(復坐標軸)上的分布如下所示：

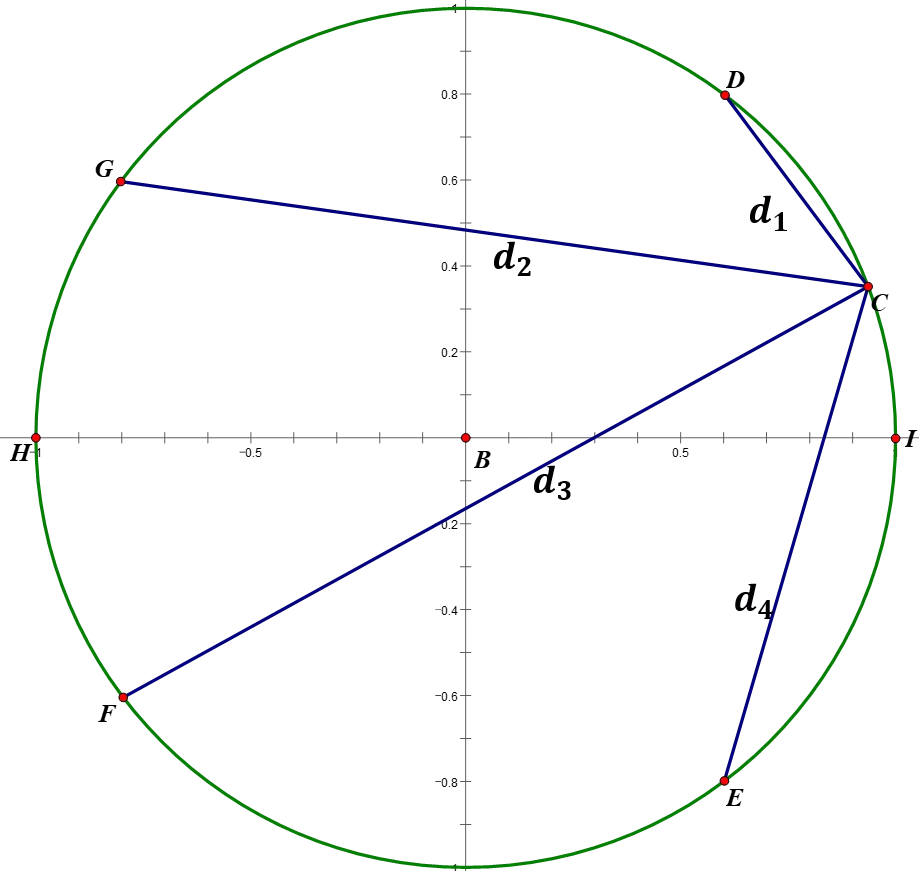
易得五元陣的陣因子模值可表示為：

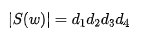
圖中當自變量點w位于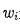和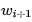兩個零點的中間位置時，S|(W)|就可近似看為第i個副瓣的峰值。主瓣區在點D和點E之間，I點為最大值點，其余零點間的區域為副瓣區。如果能使四個零點都往H點靠近，那么副瓣肯定會降低，同時容易看出主瓣區域變大，主波束寬度增加，從而導致增益下降。

道爾夫-切比雪夫綜合法

由于常規的陣列天線，其副瓣電平較高。為了使雷達系統具有較高的抗干擾、抗反輻射導彈等的能力，往往要求對陣列天線的幅度進行加權以實現低副瓣特性。采用道爾夫—切比雪夫綜合法、泰勒綜合法等設計的陣列天線就可實現低副瓣。

本節講述一種在實際工程中常用的陣列天線綜合方法——道爾夫-切比雪夫綜合法。

切比雪夫陣列的特點是 ：

(1)  等副瓣電平；  

(2)  在相同副瓣電平和相同陣列長度下主瓣最窄，稱為最佳陣列； 

(3)  單元數多，且副瓣電平要求不是很低時，陣列兩端單元激勵幅度跳變大，使饋電困難。

在這里簡單介紹下切比雪夫多項式：

·切比雪夫多項式在逼近理論中有重要的應用。這是因為第一類切比雪夫多項式的根（被稱為切比雪夫節點）可以用于多項式插值。相應的插值多項式能最大限度地降低龍格現象，并且提供多項式在連續函數的最佳一致逼近。

百度百科

在微分方程的研究中，數學家提出切比雪夫微分方程：

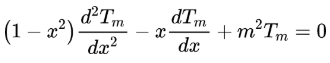
第一類切比雪夫多項式由以下遞推關系確定：

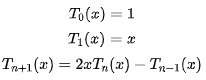
下面通過MATLAB軟件編程繪制前四項切比雪夫多項式：

x=-1.5:0.01:1.5; T1_x=x; T2_x=2*x.^2-1; T3_x=4*x.^3-3*x; T4_x=8*x.^4-8*x.^2+1; h1=plot(x,T1_x,'r','linewidth',3); hold on; h2=plot(x,T2_x,'g','linewidth',3); h3=plot(x,T3_x,'b','linewidth',3); h4=plot(x,T4_x,'c','linewidth',3); axis([-1.5 1.5 -6 6]); set(gca,'linewidth',3); xlabel('x','fontName','Times New Roman','fontsize',18); ylabel('T_n(x)','fontName','Times New Roman','fontsize',18); %繪制虛線 xx=-1:0.1:1; y1=-1*ones(1,length(xx));y2=1*ones(1,length(xx)); h5=plot(xx,y1,'--k','linewidth',1); h6=plot(xx,y2,'--k','linewidth',1); yy=-1:0.1:1; x1=-1*ones(1,length(yy));x2=1*ones(1,length(yy)); h7=plot(x1,yy,'--k','linewidth',1); h8=plot(x2,yy,'--k','linewidth',1); %圖例 legend([h1,h2,h3,h4],'T_1(x)','T_2(x)','T_3(x)','T_4(x)','Location','Best'); hold off;

 

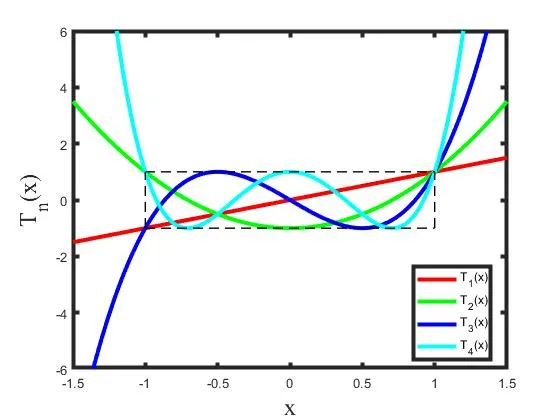
上圖給出了前四階切比雪夫多項式，從這些曲線不難發現:

• 對于  。在這個范圍內，切比雪夫多項式的函數值在  ±1之間呈現等波紋振蕩。

不過，上面給出的切比雪夫多項式只適用于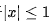的范圍；當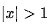時, 要滿足x=cos u, 則w必須是一個純虛數, 即u=jv(v 為實數)  。因此需要對微分方程進行變量替換：

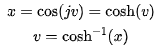
于是初始的切比雪夫微分方程可變形為：

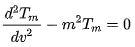
最終求得切比雪夫函數在整個x軸的解：

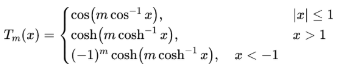
為了實現陣列天線的可控等副瓣電平，如何將切比雪夫多項式的帶內振蕩曲線作為方向圖的等電平副瓣電平呢？即怎樣使切比雪夫多項式與陣因子多項式聯系起來？

注意到切比雪夫函數的形式為 ：

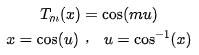
而當陣列激勵分布為對稱分布時，則導出的陣因子也可表示為的形式。

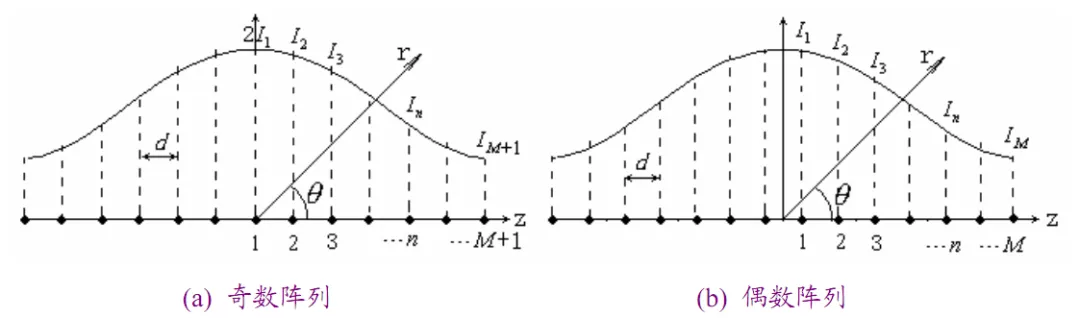
如上圖所示，奇數單元的陣列可將中間單元拆分為兩個位置重合的單元，這樣奇/偶數單元陣列導出的陣因子在形式上基本一樣。這里以奇數單元陣列(N=2M+1)為例，其陣因子為：

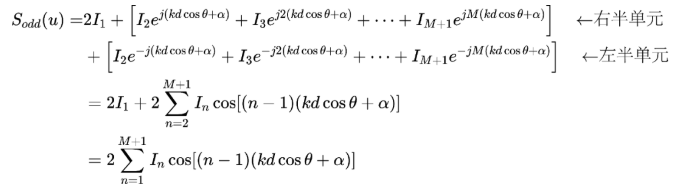
利用歐拉公式，很容易就可以將對稱的兩個單元的陣因子項相加變為cos(nu)的形式。

經過化簡，得到歸一化陣因子為：

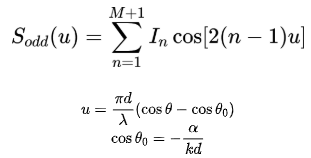
為了確定給定低副瓣指標下的各單元的激勵幅度值，后面需要采用待定系數法，巧妙地將陣因子與限定區間內呈現等波紋特性的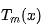函數聯系起來。

同理可得：

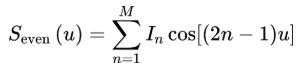
對于N=10(偶數陣，M=5)，陣因子可表示為(另一半對稱，左右滑動公式查看全貌)：

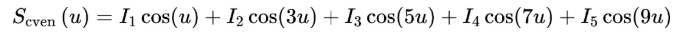
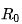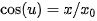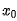無量綱形式的主副瓣比為，采用用變量代換令，其中滿足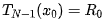。這樣將cos(nu)用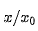進行替換并展開 :

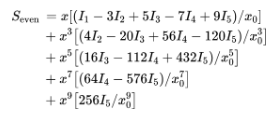
令(左右滑動公式查看全貌)：

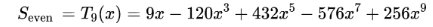
比較同類項系數，解線性方程組即可得出能實現給定主副瓣比，對應的的值。

實例操作

經過簡單的編程后，我們可以綜合單元數大于3的線陣，求得其切比雪夫幅度加權對應的激勵單元饋電幅度分布。MATLAB p文件代碼附在文末的下載鏈接。

運行該p文件后，計算10單元，30dB低副瓣情況下對應的激勵幅度分布為：

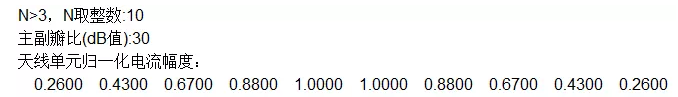
在淺談陣列天線及布陣中仿真過一個微帶貼片線陣：

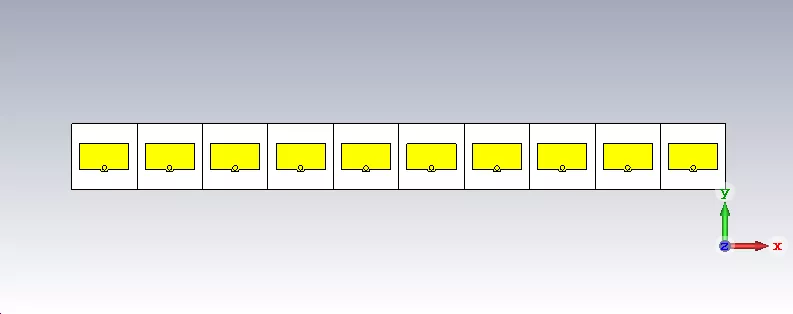
當單元個數為10，且全激勵的情況下其主副瓣比還是比較高的，因此我們將上面的切比雪夫加權對應的幅度值設置給各天線單元激勵端口。

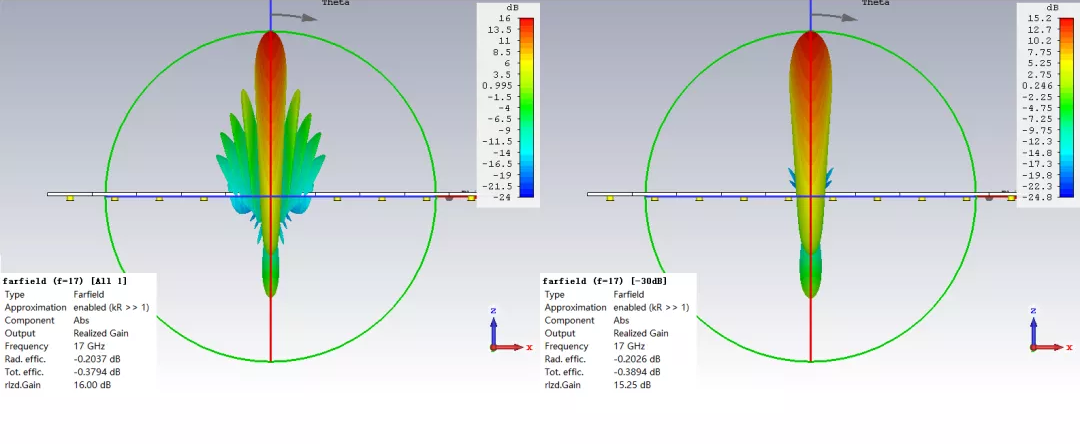
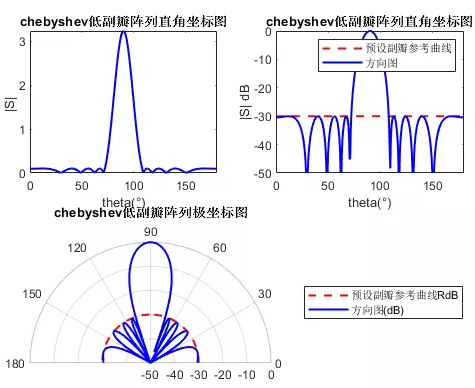
從下面對比結果不難看出，經過切比雪夫幅度加權后的10單元線陣，其相對副瓣電平從原來的-13.25dB下降到了-30dB。不過天線的實際增益也因此少了0.75dB，也算是有得必有失吧。（由于線陣的地板不夠大，因此其后瓣較高，因此這個實例中我們主要觀察主瓣和第一副瓣的差值）

 

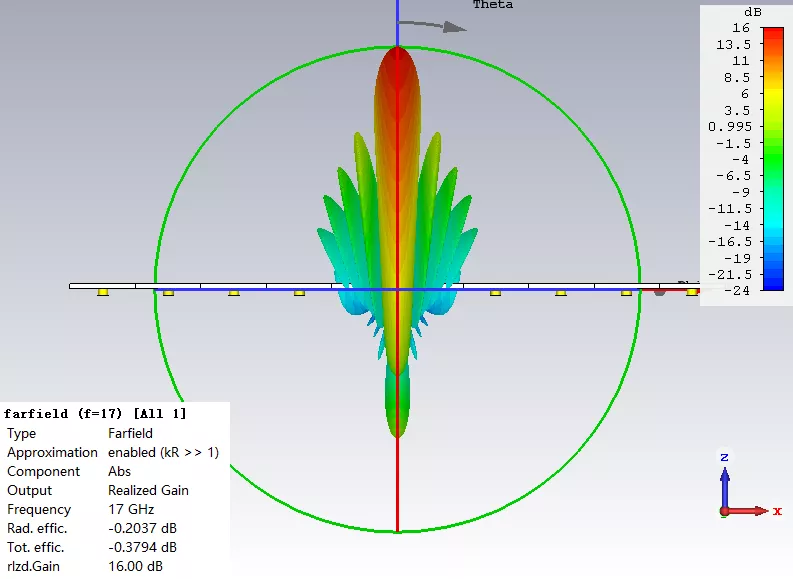
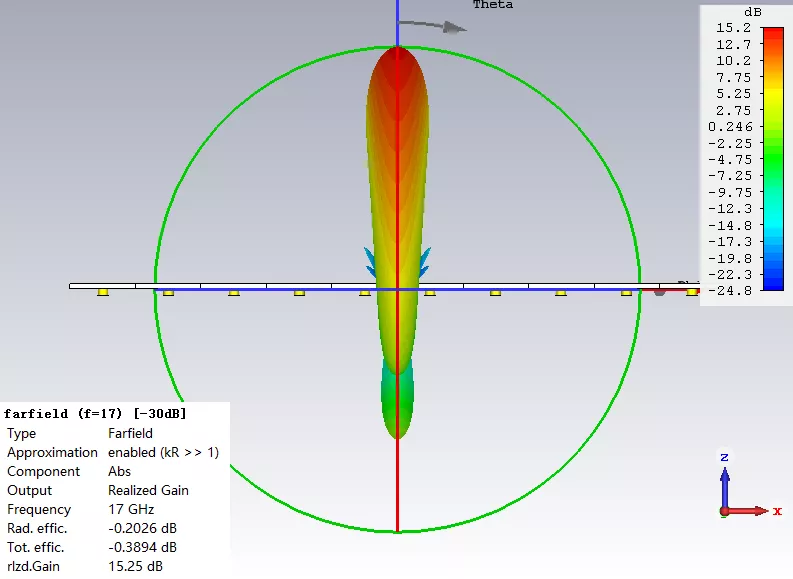
左圖為等幅度激勵

右圖為切比雪夫幅度加權

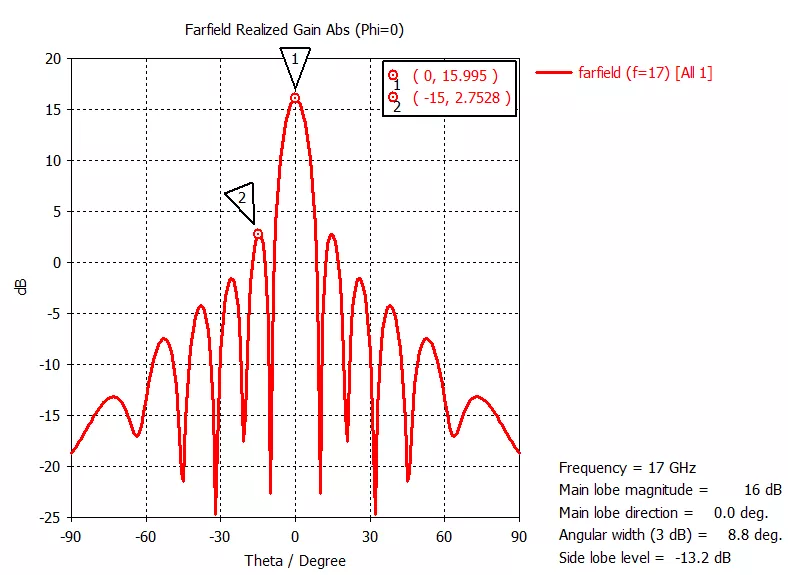
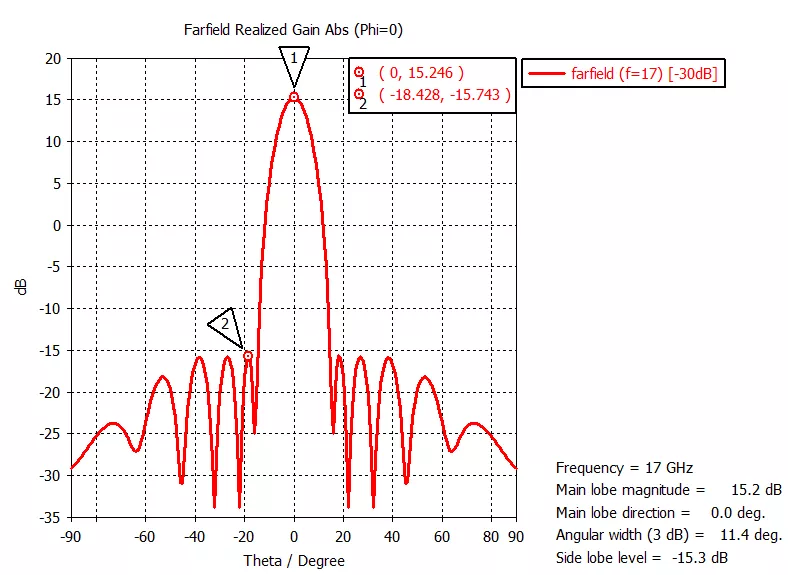
左圖為等幅度激勵

右圖為切比雪夫幅度加權

當然，你也可以嘗試綜合20，30單元的低副瓣，仿真相應的線陣進行幅度加權，看看實際得到的副瓣是否還滿足需求。

資源分享

PDF文件在下面的總文件夾進行更新：低副瓣陣列的設計原理

https://pan.baidu.com/s/1wi7BcSFhpvdU6lvb2vFqcg

提取碼：q8ra

END

本文為MWRF.NET原創文章，未經允許不得轉載，如需轉載請聯系market#mwrf.net(#換成@)