“你認(rèn)為最美的數(shù)學(xué)、物理方程是什么？”當(dāng)代十位大數(shù)學(xué)家、物理學(xué)家給出了他們自己的回答。這些回答構(gòu)成了大雅之美（The Concinitas Project）的十篇文章。我們?yōu)樽x者帶來這些大師對自己眼中最美方程的精彩解讀。

1.指標(biāo)定理

撰文 阿蒂亞爵士（Sir Michael Atiyah）

翻譯 邵紅亮（重慶大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院）

校譯 林開亮

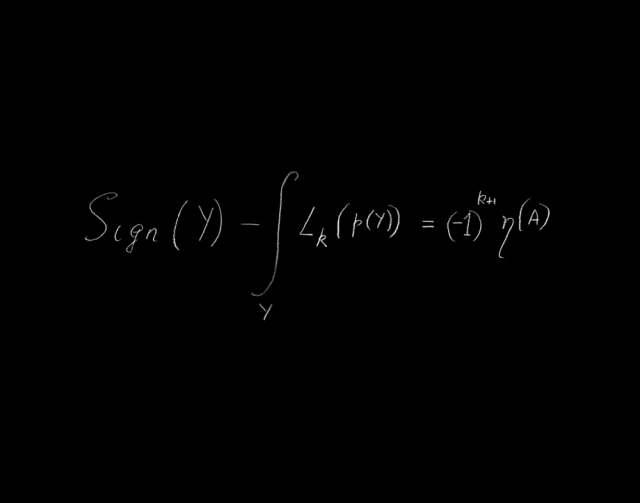
?數(shù)學(xué)既是一門藝術(shù)，也是一門科學(xué)，而美在其中扮演至關(guān)重要的角色，這是數(shù)學(xué)家眾所周知的事實(shí)。偉大的德國數(shù)學(xué)家赫爾曼·外爾（Hermann Weyl）是我心目中的英雄。他說：“我的工作總是試圖將真和美統(tǒng)一起來，如果我必須做出抉擇，我常常選擇美。”我覺得他講得非常好。

數(shù)學(xué)是最精準(zhǔn)的科學(xué)，它致力于發(fā)現(xiàn)真理，外爾的話似乎有些荒誕，甚至帶有挑釁的感覺——似乎只是一句半開玩笑的話。但是我相信，外爾講這句話時是非常認(rèn)真的。在外爾的話中有一個明顯的悖論，我們尋求的雖然是客觀真理，可是任何時候，真理都是不確定的，是暫時的。然而美是一種主觀體驗(yàn)，“情人眼里出西施”，我們相信，美是指引我們找到真理的光亮。

何為數(shù)學(xué)之美？是否與藝術(shù)之美、音樂之美、詩歌之美類似？維爾斯特拉斯（Karl Weierstrass）表面上是一個嚴(yán)肅的分析學(xué)家，卻曾經(jīng)說過：“如果沒有一顆詩人般的靈魂，就不可能成為完全的數(shù)學(xué)家。”

對門外漢而言，這樣的表達(dá)是難以理解的，然而我也曾經(jīng)說過，著名的歐拉公式

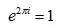
極其簡潔且極具深度，無異于哈姆雷特的著名問題，“活下去還是不活……”

也許最可與數(shù)學(xué)比肩的一種藝術(shù)形式就是建筑了，其中有充滿精美細(xì)節(jié)的宏觀視野，實(shí)體基礎(chǔ)和功能效用都是其本質(zhì)組成。

我選擇這樣一個方程來闡釋我自己的工作美妙之處，它宏偉壯觀，富有歷史，與數(shù)學(xué)的許多分支有多重聯(lián)系，包括：拓?fù)洹缀巍⒎治觥５瞧浔硎鲋⒚睿浜啙嵭裕谷藗兒雎粤搜谟谄渲械纳疃龋挥姓嬲I(lǐng)會的學(xué)者方能明白。

就像一座有三層塔的建筑，這個方程有三項(xiàng)，這三項(xiàng)各自屬于數(shù)學(xué)的不同部分，卻以一種驚人的方式聯(lián)系在一起。就像偉大的建筑一樣，它也有自己的特征，可以追根溯源至很久以前，展現(xiàn)了當(dāng)今最先進(jìn)的技術(shù)，同時又指向未來。

這個方程的前身與歷史上許多主流問題都有聯(lián)系：歐拉的柯尼斯堡七橋問題、黎曼素?cái)?shù)計(jì)數(shù)以及高斯測地。這些故事充滿詩意，然而未來與歷史同樣重要。許多主流分支已經(jīng)消失，只有少數(shù)綿延至今。

大約四十年前，我發(fā)現(xiàn)了這個方程，自那時起，人們就發(fā)現(xiàn)它在基礎(chǔ)物理中有的令人神魂顛倒的驚人應(yīng)用，這一點(diǎn)外爾應(yīng)該是理解的，并且會很欣賞。事實(shí)上，其中許多關(guān)鍵的想法，都可以追溯到外爾本人的工作。

就我個人而言，我的方程體現(xiàn)了我與諸多同事的深入合作，包括：波恩的赫茲布魯赫（Fritz Hirzebruch），哈佛的博特（Raoul Bott），MIT的辛格（Is Singer）和孟買的帕托迪（Vijay Patodi），像許多天才詩人一樣，帕托迪也英年早逝。美是一種人生體驗(yàn)，最美不過與朋友共賞。

（邁克爾·阿蒂亞爵士（Sir Michael Atiyah），英國數(shù)學(xué)家，菲爾茲獎和阿貝爾數(shù)學(xué)獎得主，曾任皇家學(xué)會主席，劍橋大學(xué)三一學(xué)院院長。他與伊薩多·辛格合作證明了著名的阿蒂亞-辛格指標(biāo)定理。此定理在微分方程、復(fù)幾何、泛函分析以及理論物理學(xué)中均有深遠(yuǎn)的應(yīng)用，公認(rèn)為20世紀(jì)最重要的數(shù)學(xué)成果之一。）

2.安培定律

撰文 唐納森（Simon Donaldson）

翻譯 來米加（上海交通大學(xué)數(shù)學(xué)科學(xué)學(xué)院）

校譯 林開亮

?我的很多研究工作涉及微分幾何中和數(shù)學(xué)物理相關(guān)的一些課題與四維空間拓?fù)涞慕徊妗：诎迳系膬?nèi)容，是想部分地通過與三維空間類比，來闡明其中的一些想法。

圖示的主題是電磁學(xué)的安培定律，這圖大概跟讀者在標(biāo)準(zhǔn)物理課本中所見的類似。左上用粗體白線表示電流J流過一個封閉線圈。小的箭頭則表示電流所產(chǎn)生的磁場B。在二維，這對應(yīng)于將鐵屑散落在一張紙上所形成的圖樣。磁場在每點(diǎn)都有定義，因此我們應(yīng)該想象，每一點(diǎn)都有一個小箭頭表示磁場，只不過在圖示時我們只畫出一些作示意。上圖中這個基本的物理現(xiàn)象，用普通的語言來陳述就是，電流產(chǎn)生的磁場方向“環(huán)繞”線圈，安培定律則對此給出了一個精確的定量刻畫。

向量場這個概念，比如磁場（或者電流，看作被局限為沿著線圈），是19世紀(jì)早期數(shù)學(xué)物理中一個非常重要的觀念進(jìn)展。它為描述電、磁、重力等提供了一個統(tǒng)一的框架。這其中有一個重要的概念是，向量場通過某一曲面的通量。數(shù)學(xué)上，這個定義由曲面積分給出；而直觀上，可以把向量場想象成某個流體在每點(diǎn)的流速，那么通量就是流體流過該曲面的流速。

安培定律的 “積分形式”可表述為：由電流產(chǎn)生的磁場繞一曲面的邊界曲線的環(huán)量，等于電流通過該曲面的通量。黑板中心橫穿線圈的小圓盤給出了這樣一個曲面的示意。安培定律的“微分形式”，就是黑板右下方的一組方程：電流在空間坐標(biāo)x,y,z下的三個分量，可以分別表為磁場在空間坐標(biāo)x,y,z下的三個分量的導(dǎo)數(shù)之組合。

我想用黑板上的內(nèi)容傳達(dá)出，我所認(rèn)為的數(shù)學(xué)中的一些非常美妙的方面。左邊是圖片和文字，右邊是一組方程。他們是同一個事物的不同描述，引發(fā)不同角度的理解：圖形的和符號的。更進(jìn)一步，這個圖示代表一個具體的物體——真實(shí)世界中的一個帶電流的銅線圈。數(shù)學(xué)家畫類似的示意圖，但是它可以不僅僅代表一個在三維空間中的一維線圈。通過想象，它也可以代表一個在七維空間中的三維對象，甚至是在無窮維空間中的對象。這種從我們物理直覺到抽象情形的拓展，具有顯著的有效性。在頭腦中，這種直覺的、圖形的、符號的和抽象的交互思維，非常美妙且令人愉悅。

所有這些和拓?fù)鋵W(xué)（一種研究對象在連續(xù)形變下保持不變的性質(zhì)的學(xué)科）又有什么關(guān)系呢？示意圖中，打結(jié)的閉合線圈暗示著這種聯(lián)系。一個扭結(jié)就是一個封閉線圈，但你無法通過連續(xù)形變（即不允許剪開和粘合）把它變?yōu)闃?biāo)準(zhǔn)的圓圈。這是一種我們憑經(jīng)驗(yàn)可以理解、但在數(shù)學(xué)上不容易講清楚的概念。很容易想見，這樣的扭結(jié)可以極其復(fù)雜，從而使得拓?fù)鋵W(xué)變得相當(dāng)微妙。具體來說，存在一種扭結(jié)到四維空間的聯(lián)系：扭結(jié)自身暗含了一種信息，它指明如何按一定的方式將標(biāo)準(zhǔn)四維空間構(gòu)建粘合成一個新的四維空間。

黑板所示當(dāng)然更多地側(cè)重于思想而非背后精確的數(shù)學(xué)。它想傳遞的思想是，研究一個扭結(jié)閉合電路產(chǎn)生的磁場，是與扭結(jié)以及四維空間的拓?fù)溆嘘P(guān)聯(lián)的。在過去的三十年間，確有許許多多契合這種思想的研究進(jìn)展，盡管其細(xì)節(jié)不盡相同。例如，這些發(fā)展涉及將電磁場論推廣到“楊－米爾斯場”，以及與量子力學(xué)、量子場論建立聯(lián)系。這一點(diǎn)用左下角的磁場通過一個小圓盤的通量來示意。（就作者所知）這個量在經(jīng)典的電磁學(xué)中沒有什么意義，但在磁場與電子的“波函數(shù)”相互作用的量子理論里是核心。

三維和四維有什么特殊之處呢？這在拓?fù)鋵W(xué)中是個深刻的問題。結(jié)果表明，維數(shù)大于4的空間在許多方面都更容易理解。我們甚至無需搞清楚問題的具體含義，就可以通過所展示的方程式來體會三維的特殊性。右邊后兩個方程可以由循環(huán)重排頭一個方程的三個坐標(biāo)x,y,z依次得到。這依賴于x,y,z中恰有三個對：(xy),(yz),(zx)。我們可以把電磁學(xué)形式地推廣到高維，但這樣磁場就不再是一個向量場，而是一個更復(fù)雜的對象。三維的特殊性就在于，磁場和電場同樣都是向量場。四維中有類似的推廣，也是基于四維特殊的拓?fù)湫再|(zhì)。從本質(zhì)上理解這些，是一個極迷人的問題，而我們目前大概也只是看到了最終真理的一些影子罷了。在這里，我們還從中發(fā)現(xiàn)了數(shù)學(xué)的另一個美妙所在：不同領(lǐng)域之間產(chǎn)生的令人驚訝而神秘的聯(lián)系，以及交織在那些看似簡單并充分理解中的完全未知的存在。

（西蒙·唐納森（Simon Donaldson），英國數(shù)學(xué)家、倫敦帝國學(xué)院教授。他是菲爾茲獎得主，并獲得了邵逸夫獎和數(shù)學(xué)突破獎。他找到了四維流形的系列不變量，進(jìn)而發(fā)現(xiàn)特定的四維流形容許無窮多個微分結(jié)構(gòu)。）

3.牛頓法

撰文 史蒂文·斯梅爾（Stephen Smale )

譯者 崔繼峰（內(nèi)蒙古工業(yè)大學(xué)理學(xué)院）

校譯 賈挺杰、邵美悅

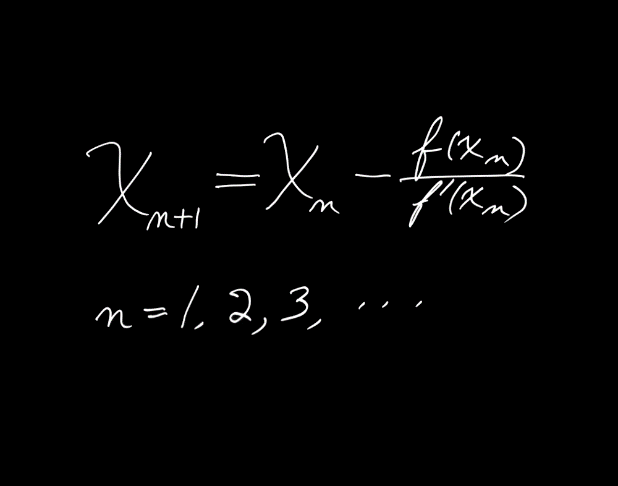
?上圖中的表達(dá)式是牛頓法的一個數(shù)學(xué)描述。

早在牛頓之前，希臘人就用這一想法來求一個正數(shù)的平方根。自牛頓以后，人們常常用它迭代以求出方程f(x)=0的近似解。在我的早期數(shù)學(xué)生涯中，一個令我非常著迷的問題是：這個迭代法何以如此快速和有效，它的局限性又是什么？

在f是一個多項(xiàng)式的特殊情況下，代數(shù)基本定理斷定方程f(x)=0有解。其解x可能是一個實(shí)數(shù)或者是一個虛數(shù)。在19世紀(jì)早期，高斯給出了上述定理的的一個基于算法的證明，該算法可以通過多次應(yīng)用牛頓法來完成（不過他的證明有一處漏洞）。我1981年的文章《代數(shù)學(xué)基本定理和復(fù)雜性理論》（The Fundamental Theorem of Algebra and Complexity Theory）就是基于牛頓方法，并與高斯的想法有關(guān)聯(lián)。

復(fù)雜度（的計(jì)算）理論也許是計(jì)算機(jī)科學(xué)中的中心議題；在該理論中，稱某個問題是可馴服的（tractable），就是說，存在一個能求解此問題的多項(xiàng)式時間算法，這里的多項(xiàng)式時間是指，用比特來衡量的運(yùn)算數(shù)目可以被輸入的數(shù)據(jù)的數(shù)目的一個多項(xiàng)式控制。一方面，我覺得復(fù)雜度的觀念很有啟發(fā)性；而另一方面，我發(fā)現(xiàn)，用這個框架并不能分析牛頓法的復(fù)雜度。

在上面提到的文章中，我用算術(shù)運(yùn)算的數(shù)目以取代比特運(yùn)算的數(shù)目，來度量牛頓法的復(fù)雜度。此外，數(shù)值分析中“條件數(shù)”的概念，在我對代數(shù)學(xué)基本定理的算法分析中，發(fā)揮了重要作用。在這個新觀點(diǎn)下，我證明了牛頓法是可馴服的。

尋找一個多項(xiàng)式零點(diǎn)的問題，可以自然地推廣到一個多項(xiàng)式方程組的求解問題。在處理這個一般問題時，我與邁克·沙勃（Mike Shub）合作，發(fā)表了《貝祖定理的復(fù)雜性》（Complexity of Bezout's Theorem）的系列論文。我們的目標(biāo)是，通過找到一種能在多項(xiàng)式時間內(nèi)求出近似解的算法，使該問題可馴服。遺憾的是，我們的努力以失敗告終，直到今天，它仍然是一個重要的公開問題。然而，彼得·比爾吉斯?fàn)枺≒eter Burgisser）和菲利普·卡克（Felipe Cucker）最近發(fā)表于《數(shù)學(xué)年刊》（Annals of Mathematics）的文章，已經(jīng)很接近該問題的解（注釋1）。研究中，他們借鑒了卡洛斯·貝爾特蘭（Carlos Beltran）和路易斯·帕爾多（Luis Pardo）的研究思路，同時，牛頓法在他們的工作中無疑發(fā)揮了重要作用。

蘭諾·布萊姆（Lenore Blum）加入了我和邁克·沙勃的團(tuán)隊(duì)，我們一起將計(jì)算機(jī)科學(xué)的圖靈機(jī)一般化，給予求零點(diǎn)研究以基本支持。我們的三人項(xiàng)目的相關(guān)實(shí)數(shù)算法已根植于多項(xiàng)式時間，NP-完全性，可馴服性的環(huán)境，這一切非常有意義。最終，菲利普·卡克與我們合作撰寫了著作《復(fù)雜性與實(shí)計(jì)算》（Complexity and Real Computation）。對此，一個參考文獻(xiàn)是我的論文集第3卷（共650頁）。

約翰·濟(jì)慈（John Keats）寫道，“美即真，真即美……”他還寫道“美的東西永遠(yuǎn)是賞心悅目的。”我在此補(bǔ)充一點(diǎn)，美是簡潔和深刻的。我希望，我的片言只語會使你相信，牛頓法是大美的體現(xiàn)。

（史蒂文·斯梅爾（Stephen Smale )，美國數(shù)學(xué)家，菲爾茲獎和沃爾夫獎得主。他成功解決了微分拓?fù)鋵W(xué)中的高維龐加萊猜想，并創(chuàng)立了現(xiàn)代微分動力系統(tǒng)理論。

1.譯者注：這個問題是斯梅爾1998年提出的18個問題（Smale's problems，見維基百科）中的一個，在2016年已經(jīng)解決（而不是像前面說的“未解決”），見Lairez, Pierre , A deterministic algorithm to compute approximate roots of polynomial systems in polynomial average time, Found Comput Math (2016)，1-28.）

4.P=NP？

撰文 理查德·卡普（Richard M.Karp）

翻譯 龍旸靖（上海交通大學(xué)數(shù)學(xué)科學(xué)學(xué)院）

?計(jì)算復(fù)雜度理論是理論計(jì)算機(jī)科學(xué)的一個分支，它主要關(guān)心機(jī)器計(jì)算效率的極限。計(jì)算復(fù)雜度理論主要研究需要大量的計(jì)算步驟來求解的問題。這些問題的輸入和輸出取自有限字母表中的字符串；輸入的長度不受限制。研究一個計(jì)算問題的核心是將其所需的計(jì)算步驟表達(dá)為以輸入的長度為自變量的函數(shù)。

有些計(jì)算問題的步數(shù)的增長速度非常快。以獨(dú)立集問題為例。該問題中圖是由一些點(diǎn)和線構(gòu)成的對象，其中點(diǎn)稱之為頂點(diǎn)，線稱之為邊。對于一個給定的圖，如果某個由其部分頂點(diǎn)構(gòu)成的集合中不存在有邊相連的兩個頂點(diǎn)，我們稱這個頂點(diǎn)集是獨(dú)立的。獨(dú)立集問題即給定一個圖和一個正整數(shù)n，判定這個圖是否包含大小為n的獨(dú)立集。所有已知的解決獨(dú)立集問題的算法都有“組合爆炸”現(xiàn)象，即所需要的計(jì)算步數(shù)以圖的大小的指數(shù)級函數(shù)增長。另一方面，給定的頂點(diǎn)集是否是給定圖的獨(dú)立集卻很容易檢查。有很多問題都有這樣的二分性：即很難判定一個給定結(jié)構(gòu)類型是否存在（存在性問題），卻很容易判定給定的結(jié)構(gòu)是否為所求的類型（驗(yàn)證性問題）。

解決存在性問題比解決其對應(yīng)的驗(yàn)證性問題困難是一個共識。例如，似乎很難決定一個拼圖是否可解。但是給定拼圖塊的順序，很容易驗(yàn)證其是否為一解。同樣，數(shù)獨(dú)問題似乎很難解，但是很容易驗(yàn)證給定的解。計(jì)算復(fù)雜度理論中給出了P和NP的精確定義：P問題是容易解決的存在性問題類，而NP問題 是容易驗(yàn)證解的存在性問題類。人們一般認(rèn)為驗(yàn)證解比給出解要容易，因此似乎NP類真包含P類。但是這個論斷還沒有證明。P=NP是否成立是理論計(jì)算機(jī)領(lǐng)域核心的未解決問題（注釋2），并且是所有數(shù)學(xué)分支中最難的問題之一（注釋3），因其難解而聞名于世。

1972年我在一篇題為“組合問題之間的互約性”的文章中提出了一種數(shù)學(xué)技術(shù)，用它能證明成千上萬個從數(shù)學(xué)、科學(xué)、工程、商業(yè)和日常生活中產(chǎn)生的計(jì)算問題是等價的。這里等價是指其中一個問題的有效的算法能生成其他所有NP問題的有效算法，因此如果P=NP，則問題完全解決，相反，如果P不等于NP，那么這些問題都不容易解決。這類問題被稱為NP完全問題。NP完全是一個廣泛發(fā)生的現(xiàn)象，大多數(shù)應(yīng)用中產(chǎn)生的組合問題屬于NP完全類，因此，它們極有可能很難解決。

我提出的這一數(shù)學(xué)技術(shù)源于多倫多大學(xué)的庫克（Stephen Cook）在1971年的一篇文章，這篇文章中證明了一個特定的問題，即命題邏輯中的限制性滿足問題（記為Sat）是NP完全的。他證明了任何NP類中的問題可以有效規(guī)約到Sat，即對于任意NP問題A，存在一個有效算法可以把A中的任何實(shí)例轉(zhuǎn)化成一個Sat中等價的實(shí)例。因此，如果Sat容易解決，則每一個NP問題都容易解決。差不多同時，當(dāng)時在蘇聯(lián)，現(xiàn)在是波士頓大學(xué)教授的萊文 （Leonid Levin）也證明了一個類似的結(jié)果。

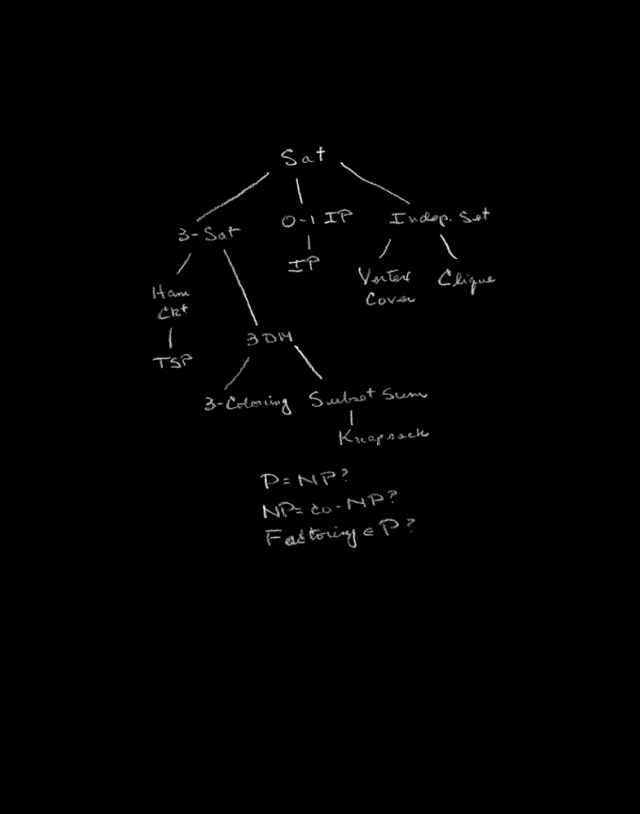
在一篇1972年的文章中，我用有效規(guī)約樹來證明21個經(jīng)典問題是NP完全的，從而證實(shí)了NP完全問題的普遍存在。主題圖通過規(guī)約樹展示了其中的13個問題之間的規(guī)約。規(guī)約樹的每一個的節(jié)點(diǎn)上標(biāo)記一個NP問題，每一條邊表明上面的問題可以有效規(guī)約到下面的問題，要是下面的問題容易解決，則上面的問題也容易。如果這棵樹上的所有問題都是容易解決的，那么Sat問題就是容易解決的，因此，由庫克的開創(chuàng)性結(jié)果可知，任何NP類中的問題都是容易解決的。

復(fù)雜度理論學(xué)家中比較盛行（并非全體接受）的看法是，P不等于NP，但是目前還沒有證明或者反證。也許某些聰明的年輕人受這篇論文的啟發(fā)，會找到攻克N和NP難題的辦法。

數(shù)學(xué)之美存在于多個層面：在對稱而精妙的數(shù)學(xué)曲線中、在曲面和組合結(jié)構(gòu)中，也在邏輯微妙的數(shù)學(xué)證明中，抑或，如NP完全一例中，發(fā)現(xiàn)隱藏在看似無關(guān)的數(shù)學(xué)現(xiàn)象背后的單一準(zhǔn)則，也美妙非凡。

（理查德·卡普（Richard M.Karp），計(jì)算機(jī)科學(xué)家，圖靈獎得主，加利福尼亞大學(xué)伯克利分校教授。他在算法方面有許多貢獻(xiàn)，尤其是“NP-完全”問題。

2.原文為open question,在數(shù)學(xué)上也譯為“公開問題”或者“開放問題”。有公開征集解的含義。

3.理論計(jì)算機(jī)領(lǐng)域被認(rèn)為是數(shù)學(xué)領(lǐng)域的一個分支。）

5.守恒律

撰文 拉克斯（Peter Lax）

翻譯 龍旸靖（上海交通大學(xué)數(shù)學(xué)科學(xué)學(xué)院）

校譯 劉云朋

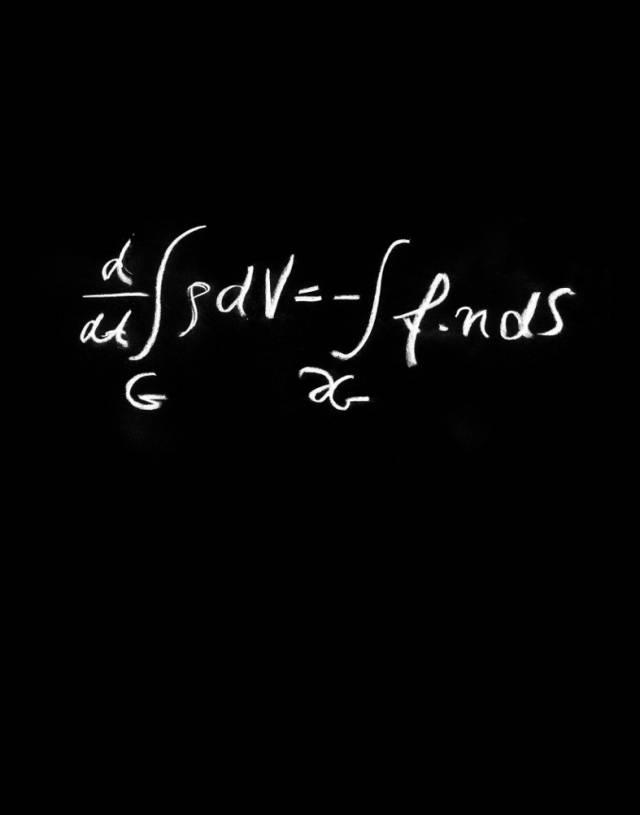
?守恒律是指某物理量(如質(zhì)量、動量、能量等)在任何區(qū)域中的總量的增長率都等于單位時間內(nèi)從該區(qū)域的邊界流入的或者產(chǎn)生的這種物理量的多少。這個思想因其基本而美。一旦將其細(xì)節(jié)具體化，就會得到很多不同的現(xiàn)象。支配流體的流的定律就是守恒律。

守恒律是理解沖擊波的關(guān)鍵。我于1945年在部隊(duì)的時候開始接觸沖擊波。當(dāng)時我被派去Los Alamos參與（美國）原子彈計(jì)劃，而沒有去太平洋參與入侵日本，因?yàn)樵訌椕馊チ巳肭秩毡镜谋匾Ｔ訌棽荒芡ㄟ^試錯的辦法來制造，所以算出炸彈引爆時產(chǎn)生的流極其重要。馮·諾依曼（Von Neumann）意識到這種計(jì)算非依賴計(jì)算機(jī)不可，這是他支持計(jì)算機(jī)的最初動力。當(dāng)然他也意識到計(jì)算機(jī)在設(shè)計(jì)原子武器外的其他方面的重要性。

馮·諾依曼在數(shù)值計(jì)算中把沖擊波看作流體的一部分，而非其邊界，這是一個美妙而原創(chuàng)的想法。這樣處理帶有沖擊波的流既有力又簡單。許多人不知道，馮·諾依曼不僅僅是20世紀(jì)的理論數(shù)學(xué)家，而且是一位頂尖的應(yīng)用數(shù)學(xué)家。

（彼得·拉克斯（Peter Lax），匈牙利裔美國數(shù)學(xué)家，阿貝爾獎得主，在可積系統(tǒng)、流體動力學(xué)和激波、孤波物理學(xué)、雙曲守恒律等領(lǐng)域都取得了重大成就。）

6.十三？

撰文 大衛(wèi)·芒福德（注釋4）（David Mumford）

翻譯 陳見柯（中國傳媒大學(xué)）

校譯 林開亮

數(shù)學(xué)家們一大部分的工作是在研究那些經(jīng)推理而得的“對象”，使其變得像我們?nèi)粘Ｉ钜粯诱鎸?shí)，雖然它們遠(yuǎn)非實(shí)物一樣地存在。柏拉圖（注釋5）正多面體在高維情形的推廣是相對簡單的例子。人們希望能在高迪（注釋6）主持修建的圣家族大教堂（注釋7）的某個尖頂上放置正二十面體，這的確是可真實(shí)觸碰的對象。但數(shù)學(xué)家們一致認(rèn)為，空間的維數(shù)可以超過3，19世紀(jì)數(shù)學(xué)家施萊夫利（注釋8）發(fā)現(xiàn)了柏拉圖多面體在四維情形下的推廣。對此，我們只能想象。記Mg是虧格g的光滑射影曲線的模空間，很長時間里，我的一直關(guān)注于如何很好地理解其結(jié)構(gòu)。在我的學(xué)生時代，即便以數(shù)學(xué)家所謂清晰的標(biāo)準(zhǔn)來看，這類空間似乎依舊籠罩在煙霧之中，它們是一種介于成熟數(shù)學(xué)和幻象之間的存在。我一度努力改變這種狀況。

與此同時，亞歷山大·格羅滕迪克（注釋9）橫空出世。他有著前人從未具有的高度抽象的思維能力，并對人們尚未理解的具體問題予以啟發(fā)。事實(shí)證明，他深刻的結(jié)果可以應(yīng)用于長期困擾我的空間結(jié)構(gòu)問題。而那時的我卻不知該如何利用。這些結(jié)果的強(qiáng)大之處在20年后才變得明顯起來：通過與喬·哈里斯（注釋10）合作，我們終于能夠?qū)g看作真實(shí)的對象（借助標(biāo)準(zhǔn)術(shù)語，它是一個擬射影代數(shù)簇）。

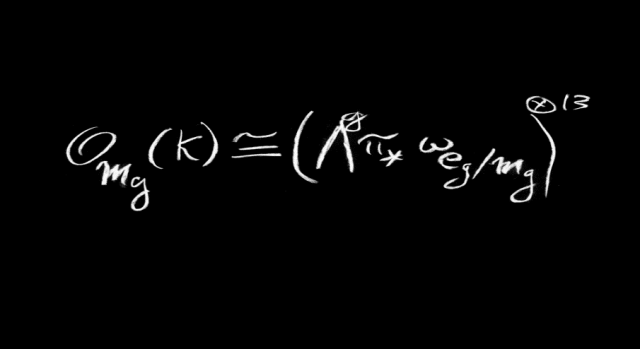
?這個公式意味著什么？它優(yōu)美在何處？它表明：兩個對象（“線叢”）本質(zhì)相同（“同構(gòu)”）。等式左邊的對象決定Mg的幾何。追溯至高斯（注釋11），人們就已經(jīng)知道空間可大致分為三種：像平面一樣的平坦空間；像球面一樣的正曲率空間；以及像馬鞍面一樣的負(fù)曲率空間（曲面上三角形內(nèi)角和小于180°）。等式左邊決定了Mg在上述三分法中的位置；博特（注釋12）將等式右邊稱為“重言”結(jié)構(gòu)：完全由Mg決定的基本對象。上述同構(gòu)表明，在g充分大的條件下，Mg是負(fù)曲率空間。

上述公式最讓人驚訝的地方是數(shù)字13。翻閱數(shù)學(xué)雜志，你會發(fā)現(xiàn)，除頁碼外，論文中一般不會出現(xiàn)大于2的數(shù)字。此處出現(xiàn)的13是計(jì)數(shù)得出的，計(jì)數(shù)問題有悠久的歷史，另一個著名的例子，是一個三次曲面上恰好有27條直線（包括復(fù)直線）。就此而言，我始終覺得造物主在跟我們開玩笑。

（4 大衛(wèi)·芒福德，David Mumford，1937年——，美國數(shù)學(xué)家。

5 柏拉圖，Plato，約公元前427年——公元前347年，古希臘哲學(xué)家。

6 安東尼·高迪，Antoni Gaudí，1852年——1926年，西班牙建筑師。

7 圣家族大教堂（加泰羅尼亞語：Basílica i Temple Expiatori de la Sagrada Família），又譯作神圣家族大教堂，簡稱圣家堂（Sagrada Família），是位于西班牙加泰羅尼亞巴塞羅那的一座羅馬天主教大型教堂，始建后由西班牙建筑師安東尼·高迪接手設(shè)計(jì)與建設(shè)。

8 路德維希·施萊夫利，Ludwig Schläfli，1814年——1895年，瑞士數(shù)學(xué)家。

9 亞歷山大·格羅滕迪克，Alexander Grothendieck，1928年——2014年，法國數(shù)學(xué)家。

10 喬·哈里斯：Joe Harris，1951年—— ，美國數(shù)學(xué)家。

11 卡爾·弗里德里希·高斯：Carl Friedrich Gauss，1777年——1855年，德國數(shù)學(xué)家。

12 拉烏爾·博特：Raoul Bott，1923年——2005年，匈牙利裔美國數(shù)學(xué)家。）

7.Ree群公式

撰文 邦別里（注釋13）（Enrico Bombieri）

翻譯 林開亮（西北農(nóng)林科技大學(xué)理學(xué)院）

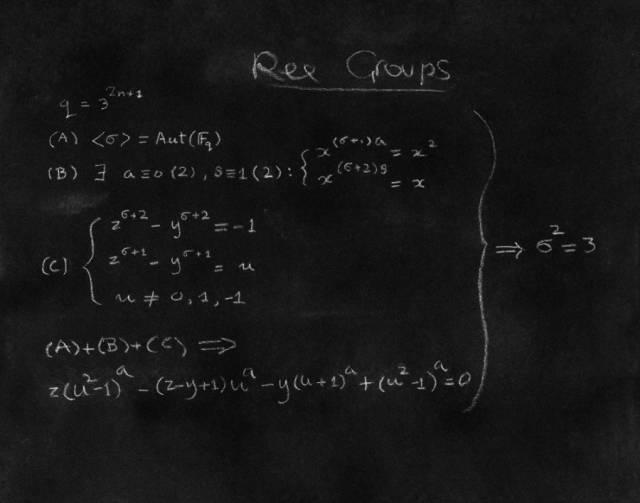
?數(shù)學(xué)中存在美嗎？這個問題關(guān)心的是數(shù)學(xué)對象及其關(guān)系，可被驗(yàn)證的證明即真正的數(shù)學(xué)對象。數(shù)學(xué)家通常會贊同，在定理和證明的結(jié)構(gòu)之中的確存在著美，即便大多數(shù)時候這種美只有數(shù)學(xué)家自己才能看得到。

群的概念漂亮地表達(dá)了數(shù)學(xué)中的對稱。群是什么？考慮任意一個對象，不論它是具體的還是抽象的。該對象的一個對稱——數(shù)學(xué)的行話叫自同構(gòu)——就是該對象到自身的一個保持它的所有性質(zhì)的映射。兩個對稱的乘積，即兩個映射的復(fù)合，仍然是一個對稱，而且每個對稱都有一個倒過來的逆。數(shù)學(xué)家認(rèn)為連續(xù)的Lie群——譬如圓周或球面的旋轉(zhuǎn)群——是很大一部分?jǐn)?shù)學(xué)和物理的漂亮基礎(chǔ)。除了連續(xù)的Lie群，還有不連續(xù)的有限群和離散群；有一些是通過將Lie群約化到一個有限或離散的框架下得到的。

群可以極其復(fù)雜。給定一個群，也許會出現(xiàn)這樣的情況，存在從該群到另一個群的一個保持乘積結(jié)構(gòu)的映射。一個群稱為單群，如果這樣一個映射的像要么是該群的一個復(fù)本要么是只有一個元素（恒同映射）的平凡群。單群是構(gòu)建所有群的基本積木，因此在研究任意群時，知道所有的單群非常重要。對稱的一般有限群首次出現(xiàn)在伽羅瓦（Évariste Galois）關(guān)于代數(shù)方程的工作中。伽羅瓦在18歲時就證明了五次一般代數(shù)方程不可通過代數(shù)操作求解，其論證要點(diǎn)是，作用在5個字母a,b,c,d,e上的偶置換（即由偶數(shù)個對換相乘得到的置換）群A5是單群。這個群是最小的非交換的單群，同時也是正二十面體的對稱群。正二十面體是一個非常漂亮的幾何對象！可以想見，單群可以描述為一些特殊幾何對象的對稱群。然而，研究一個抽象化、假設(shè)出的單群，其困難恰恰包含了從其內(nèi)蘊(yùn)性質(zhì)構(gòu)造出一個豐富的幾何對象。迄今為止，羅列出所有有限單群的分類定理的完全證明占據(jù)3000多頁篇幅，匯聚了一百多位數(shù)學(xué)家近四十年的努力。

源自Lie群的有限單群系列很容易就發(fā)現(xiàn)了，只有三個例外。這些系列不是來自實(shí)數(shù)或復(fù)數(shù)，而是來自特征為p的有限域，這里p是一個素?cái)?shù)。在特征為p的有限域里，仍然可以做普通的算術(shù)，不過，一個數(shù)用p去乘總是得到0。一切都很順利，即便可能沒那么容易，除了數(shù)學(xué)家Ree的發(fā)現(xiàn)——特征2下的Lie群B2和F4和特征3下的G2也存在額外的對稱，它們可以得到新的單群系列，今天我們稱之為twisted Ree 群——留下的問題：twisted B2群及其唯一性之前由鈴木（Suzuki）通過完全不同的方法得到，F(xiàn)4情形的唯一性也得到了，但G2情形則難以捉摸。

經(jīng)過湯普森（Thompson）的艱苦努力，G2的唯一性問題歸結(jié)為，證明特征為3的有限域上的某個滿足一組極其復(fù)雜的多元方程組的變換σ，具有性質(zhì)其平方σ2作用于x如同x3，換言之σ2=3。不幸的是，消元法的普通代數(shù)操作很快就會給出項(xiàng)數(shù)是如此之多的等式，以至于全世界所有的計(jì)算機(jī)合在一起都無法存儲下來。怎么辦？早在1973年，湯普森就引發(fā)了我對這個問題的興趣，但我迷失在公式的迷宮里。1979年，當(dāng)有限單群的分類工作達(dá)到高潮時，我再一次考察了湯普森等式。我自問：是否有必要寫下這些“不可能”的公式，也許有辦法可以繞開。利用一個奇妙的技巧，可以發(fā)現(xiàn)，通過消元能夠提取到一點(diǎn)點(diǎn)有用的額外信息，再度利用那一技巧重新消元并結(jié)合新的信息，額外的信息可以精細(xì)化。重復(fù)這個精細(xì)化過程三次，就得到了所需要的等式σ2=3，除了極少數(shù)情形需要用計(jì)算機(jī)驗(yàn)證。因此，唯一性的問題解決了，另一項(xiàng)技巧也添加到有限單群分類的證明中。（注釋14）

這個等式是用白色粉筆寫在暗藍(lán)灰色的黑板上，左邊是湯普森等式，雙箭頭指向σ2=3，意指左邊的等式蘊(yùn)含了twisted Ree群的唯一性。問題很漂亮，而所期待的解答也很簡單，因而優(yōu)美，湯普森等式具有內(nèi)在隱秘的美，因?yàn)樗从沉艘粋€群的性質(zhì)。對專家來說，避開蠻力而得到的解答也具有其自身的美。事實(shí)上，數(shù)學(xué)家在追尋其真理時——有時是自動地——以尋求美為向?qū)АＵ缭娙藵?jì)慈（Keats）所說，美即真，真即美。

（13 謝謝Sarah Jones Nelson。

11 Bombieri, Enrico. "Thompson's Problem (σ2=3).." Inventiones mathematicae 58 (1980): 77-100.）

8.MacDonald 等式

撰文 戴森（Freeman Dyson）

翻譯 林開亮（西北農(nóng)林科技大學(xué)理學(xué)院）

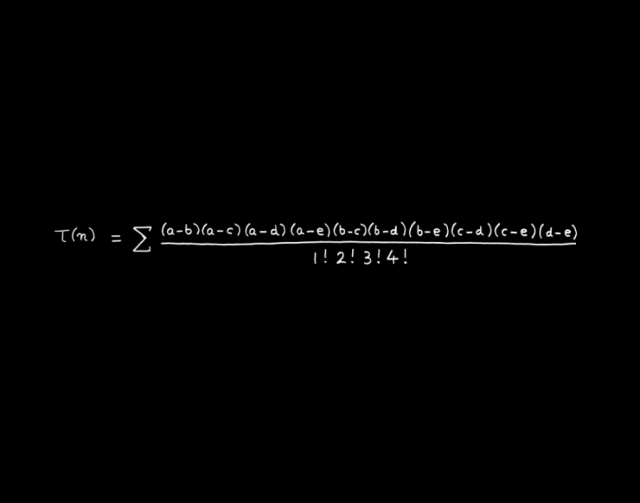
?麥克當(dāng)納（MacDonald）等式是我最美妙的發(fā)現(xiàn)。它屬于數(shù)論，這是數(shù)學(xué)中最無用和最古老的分支。我的朋友麥克當(dāng)納（Ian MacDonald）享受了第一個發(fā)現(xiàn)它的快樂，而我作為第二個發(fā)現(xiàn)者享有幾乎同等程度的快樂。我們的女兒在同一班上小學(xué)，因此我們談?wù)撐覀兊呐畠憾徽剶?shù)學(xué)。我們發(fā)現(xiàn)了τ函數(shù)滿足的一個方程，τ函數(shù)是32歲英年早逝的印度天才數(shù)學(xué)家拉馬努金（Srinivassa Ramanujan）最后四年里探究的課題。這里我寫下τ函數(shù)的麥克當(dāng)納等式。

麥克當(dāng)納等式具有神奇的五重對稱性，這一點(diǎn)逃過了拉馬努金的法眼。在等式的右邊，有十個乘在一起的差，此即五重對稱性。我們要感激拉馬努金，不僅感激他所發(fā)現(xiàn)的許多美妙的東西，還有他留給后人發(fā)現(xiàn)的其它美妙的東西。

為解釋麥克當(dāng)納等式的意義，我們來查考一下最簡單的三種情況，n=1,2,3求和取遍所有滿足條件a+b+c+d+e= 0且a2+b2+c2+d2+e2=10n的整數(shù)a,b,c,d,e。而“(mod5)”的條件意味著，a是被5除余1的數(shù)，b是被5除余2的數(shù)，c是被5除余3數(shù)，d是被5除余4的數(shù)，e是被5除余0（整除）的數(shù)。而等式中的驚嘆號含義是1!=1,2!=1×2=2,3!=1×2×3=6,4!=1×2×3×4=24。因此，當(dāng)n=1時，a,b,c,d,e只有唯一取值1,2,-2,-1,0，根據(jù)MacDonald等式，我們得到τ(1)=1。當(dāng)n=2時，a,b,c,d,e只有唯一取值1,-3,3,-1,0，我們得到τ(1)=-24。當(dāng)n=3時，a,b,c,d,e有兩種取值1,-3,-2,4,0和-4,2,3,-1,0，我們得到τ(3)=252。容易驗(yàn)證，τ(n)的這三個值與Ramanujan等式給出的值一致。

麥克當(dāng)納等式是麥克當(dāng)納發(fā)現(xiàn)的存在于兩種對稱之間的更深刻聯(lián)系的一個特殊情況。這兩種對稱我們分別稱為模對稱與仿射對稱，它們最初在科學(xué)的不同部分被發(fā)現(xiàn)，模對稱來自數(shù)學(xué)，仿射對稱來自物理。每個人都可以通過欣賞藝術(shù)埃舍爾（Mauritz Escher）畫中飛翔的天使與魔鬼而看到模對稱的展示。埃舍爾懂得數(shù)學(xué)，準(zhǔn)確掌握了細(xì)節(jié)。仿射對稱則體現(xiàn)于物理學(xué)家用高能加速器創(chuàng)造的粒子的稀有組合中。數(shù)學(xué)家朗蘭茲（Robert Langlands）第一個猜測出這些對稱與其它類型的對稱之間的聯(lián)系。麥克當(dāng)納在實(shí)現(xiàn)朗蘭茲的夢想方向上邁出了一大步。我在這里所寫下的等式僅僅是麥克當(dāng)納那一大步留下的一點(diǎn)印記。

9.電弱理論的拉格朗日密度

撰文 溫伯格（Steven Weinberg）

翻譯 劉云朋（天津大學(xué)理學(xué)院）

校譯 林開亮

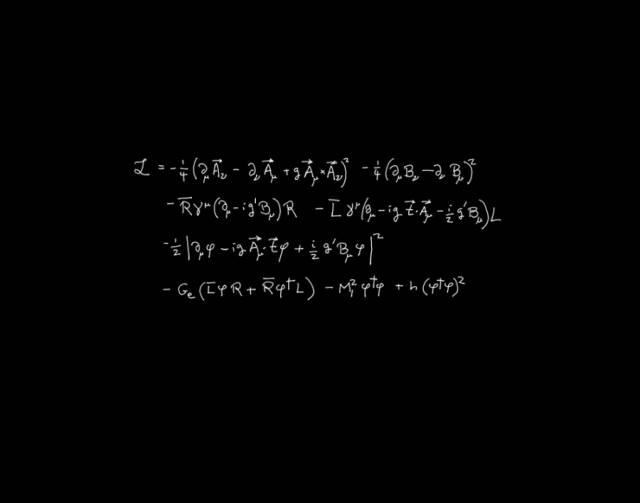
?這是方程的原始版本，后來成了自然界兩種基本的力——電磁力與弱核力——的標(biāo)準(zhǔn)理論。弱核力盡管不像電磁力那么常見，卻產(chǎn)生一種重要的放射性（β衰變）以及核反應(yīng)鏈的第一步（太陽和其它恒星賴此發(fā)熱）。我在這方面的第一篇論文發(fā)表于1967年，其中的(4)式就是這個方程。它在那幾年是基本粒子物理領(lǐng)域發(fā)表的論文中引用最多的，也許現(xiàn)在仍然如此。

電弱理論是一種場論，它的基本成分是場，其中也包括電場和磁場。方程左側(cè)的L由場及場的變化率組合而成，稱為此理論的拉格朗日密度。拉格朗日密度是像能量密度那樣的東西，根據(jù)物理學(xué)家從二十世紀(jì)三十年代就開始使用的規(guī)則，理論中各種場所遵循的方程都方便地蘊(yùn)含在拉格朗日密度之中。

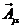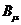方程右邊的大部分符號是理論中的各種場。弱力和電磁力由和傳遞，電場和磁場是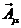和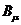的組合。中微子和左手電子場（該場描述的電子，其自旋對運(yùn)動方向的環(huán)繞與左手四指彎曲時對拇指的環(huán)繞方向一致）合在一起用L表示。右手的電子場用R表示。g 和 g’是數(shù)值常數(shù)，與電子的荷有關(guān)，其值只能從實(shí)驗(yàn)得到。

符號φ 表示某四分量的場，它與其它場相互作用，從而賦予電子質(zhì)量而使中微子仍無質(zhì)量，賦予傳遞弱相互作用的三種粒子質(zhì)量而使光子（光的粒子）仍無質(zhì)量。余下的常數(shù)Ge、M12、h 與電子的質(zhì)量、弱力的強(qiáng)度有關(guān)。φ 場的四分量之一對應(yīng)某種新的粒子，到2012年實(shí)驗(yàn)上才見到它的蹤影。方程的第三、四行描述了理論中中微子和左手電子之間、弱力和電磁力之間的對稱性破缺機(jī)制。

這個方程可能看似不大美，它美在渾然天成——給定成分后，其結(jié)構(gòu)可由數(shù)學(xué)的自洽條件很好地確定下來。略去一行，甚或只把一個負(fù)號改成正號，都會讓整體不再自洽。

方程從簡，略去了繆子（一種像電子而更重的粒子）和相應(yīng)的中微子。顯然，可以類比電子及其中微子把它們包含進(jìn)來。

1971年，此理論進(jìn)而把夸克（構(gòu)成質(zhì)子和中子的基本粒子）也包含進(jìn)來，之后不斷得到實(shí)驗(yàn)的驗(yàn)證。

10.嚴(yán)格保持的色 SU3 對稱群

撰文 蓋爾曼（Murray Gell-Mann）

翻譯 劉云朋（天津大學(xué)理學(xué)院）

校譯 林開亮

?1932年發(fā)現(xiàn)中子，人們開始認(rèn)識到原子核由中子和質(zhì)子構(gòu)成。再向它們內(nèi)部看去，可以發(fā)現(xiàn)每個中子和質(zhì)子都由三個夸克構(gòu)成——粗略地說，每種“色”一個。正是色力把夸克束縛在一起，形成中子和質(zhì)子。作為變量，色有三個不同的取值，俗稱“紅”、“綠”、“藍(lán)”。帶“色”的物質(zhì)受到禁閉，無法彼此脫離而單獨(dú)探測。在三種色互相轉(zhuǎn)換的色SU3 變換群下，物理理論完美地對稱。

這里的表達(dá)式給出“量子色動力學(xué)(QCD)”的拉格朗日密度，它用數(shù)學(xué)表達(dá)式概括了強(qiáng)相互作用的動力學(xué)。強(qiáng)相互作用同引力、弱力、電磁力一樣，都是自然界中基本的力。此表達(dá)式美在寓真實(shí)于其中。它還美在簡潔，不過是做了一點(diǎn)清理之后的簡潔。這里有三項(xiàng)，前兩項(xiàng)Lgt、Lq 分別包含膠子、夸克的貢獻(xiàn)（場），Laddl 包含“附加”項(xiàng)，其中部分的場最終預(yù)言了近期才發(fā)現(xiàn)的希格斯玻色子。

追憶往昔，我與諸同事獲得這個公式，并非靈光乍現(xiàn)，而是厚積薄發(fā)。這公式不僅總結(jié)了大自然的一個真理，還凝聚著日積月累的大量艱苦工作。它的每一項(xiàng)都薈萃了數(shù)年研究發(fā)現(xiàn)的精華。隨著時間推移，我和其他人清楚了要把哪些項(xiàng)包含其中。（我想補(bǔ)充一點(diǎn)，我們在以有點(diǎn)與眾不同的方式考慮強(qiáng)相互作用。）我們本可以在中間任何一步停下來，把更多的東西丟給“附加”項(xiàng)，但這個公式感覺很好，它很完整，滿足SU3 群所要求的對稱性條件。這條件也讓我們無法涉足當(dāng)時尚未完全探索的領(lǐng)域。所以，它盡管真實(shí)，在某種意義下卻并非終極真理，總有更多的細(xì)節(jié)可以補(bǔ)充進(jìn)去——除了希格斯，還有多種標(biāo)量場，我們知道其存在，卻不清楚如何正確描述——從而有更多的東西尚待發(fā)現(xiàn)，這也是一種美。

本文譯自：

http://www.concinnitasproject.org/portfolio/

本文原載《中國數(shù)學(xué)會通訊》2017年第1期。