作者:董名軒,香港中文大學(深圳)理工學院
1 引言
在日常工作和生活中,我們會接觸到許多不同類型的單位。比如大家熟知的國際基本單位(International System of Units, SI 單位),共有七個基本量:長度(米,m),質量(千克,kg),時間(秒,s),電流(安培,A),熱力學溫度(開爾文,K),物質的量(摩爾,mol)和發光強度(坎德拉,cd)。物理學各個領域中的其他的量,都可以由這七個基本量通過乘、除、微分或積分等數學運算導出。此外,還有一些非 SI 單位制的單位,比如在電磁學中十分常見的計量單位,分貝(decibel, dB)。它是度量兩個相同單位的數量的比例的計量單位。其中,“分(deci)”表示十分之一,“貝(bel)”則取自于美國發明家亞歷山大·格雷厄姆·貝爾(Alexander Graham Bell)。
2 感知的差異
想更好地了解分貝這個單位的起源,我們不得不從感知的差異聊起。
在 19 世紀,不同國家的物理學家和心理學家,都發現一個現象:對于人體的感知來講,心理量和物理量有一個對應關系,即同一刺激的差別量必須達到一定比例,才能引起感覺的差別。先后對這一現象進行過研究的學者們有:法國物理學家 P·布格爾、赫爾姆霍茨、德國萊比錫大學解剖學教授 E·H·韋伯、萊比錫大學物理學教授古斯塔夫·西奧多·費希納、美國發明家亞歷山大·貝爾等。
韋伯研究發現:“人類產生可查覺的最小刺激的增加的量與初始存在的刺激成正比”,它可以用一個分數來表示,這個分數雖然隨著被試的感覺不同而有變化,但對于一定的感覺來說卻是不變的。比如用手提起 1 公斤的物體時,人們可能會在重量增加到 1.2 公斤時感受出重量的差異。而當初始重量為 10 公斤時,人們可能需要在重量增加到 12 公斤時才會感受到明顯的差異。后來,韋伯的學生費希納將韋伯的研究結果總結為了數學形式: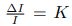 ,這便是人們所熟知的韋伯定律。其中,?I 代表刺激的差別感覺閾限(Just Noticeable Difference),I 代表標準刺激的強度,K 為一常數(又稱韋伯分數或韋伯率)。
,這便是人們所熟知的韋伯定律。其中,?I 代表刺激的差別感覺閾限(Just Noticeable Difference),I 代表標準刺激的強度,K 為一常數(又稱韋伯分數或韋伯率)。
韋伯的學生費希納在后續進一步的研究中發現,不同人對不同的刺激有不同的敏感度。他認為,主觀感覺與刺激強度的對數成正比。比如人對光和聲音的感知滿足等式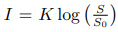 ,其中 I 為主體感受的強度,S 為刺激強度,S0 為刺激的閾值振幅,K 為一常數[12]。它說明心理量是刺激量的對數函數,即當刺激強度以幾何級數增加時,感覺的強度以算術級數增加。這被后世稱為“費希納定律”。簡單來說,這個定律說明了人的一切感覺,包括視覺、聽覺、膚覺(含痛、癢、觸、溫度)、味覺、嗅覺等,都遵從感覺不是與對應物理量的強度成正比,而是與對應物理量強度的常用對數成正比。
,其中 I 為主體感受的強度,S 為刺激強度,S0 為刺激的閾值振幅,K 為一常數[12]。它說明心理量是刺激量的對數函數,即當刺激強度以幾何級數增加時,感覺的強度以算術級數增加。這被后世稱為“費希納定律”。簡單來說,這個定律說明了人的一切感覺,包括視覺、聽覺、膚覺(含痛、癢、觸、溫度)、味覺、嗅覺等,都遵從感覺不是與對應物理量的強度成正比,而是與對應物理量強度的常用對數成正比。
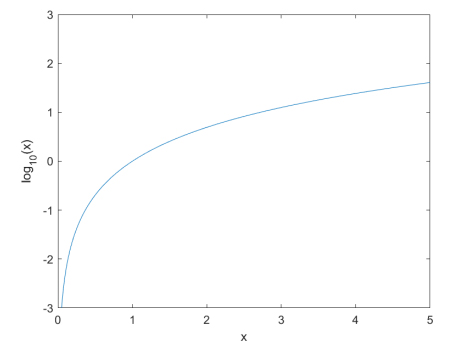
上圖是一張標準對數的曲線圖,假設 x 為刺激強度,y = log10(x) 為感受強度,切線的斜率變化為單位刺激量變化帶來的感受的變化。我們可以看到,人類對持續的、相同強度的刺激的反應會逐漸變得遲鈍。這是高速公路不會修建成一條直路的原因,需要不斷地設置緩慢的轉彎以給司機不同的刺激,降低司機因反應遲鈍造成事故的幾率。另一方面,這也是人類對自身的保護機制。在刺激量很大時,人體對于稍微改變的刺激反應較小,以保護各種感受器官;而在刺激量較小時,人類對于稍微改變的刺激反應較大,以保護身體的安全。
在這里,我們接觸到了 log,即對數運算。為了便于接下來的介紹,我們需要先了解一些對數運算的知識。
3 對數的簡單介紹
我們說對數為指數的反函數,并且稱 logb a 為“a 以 b 為底的對數”。我們可以計算任意底的對數 L = logb a,它的意思是為了得到數字 a,必須以 b 為底的冪(指數),且 bL = a 等同于(base)logarithm = number[6]。舉個例子,25 = 32,則 log232 = 5。我們常用的對數性質有:
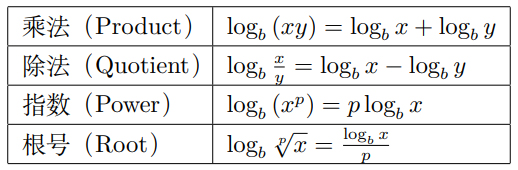
以 10 為底的對數是日常生活中最常用的對數,被稱為常用對數,可寫為 y = log x,它們的運算很方便,因為 10 的冪很容易計算[9]。除此以外,e 和 2 也是常用的底。
有了這些基礎的對數知識,我們馬上來討論分貝。我們將會了解,當使用分貝單位時,能使工程運算,尤其是涉及特別大或特別小的比量時,變得非常簡單。
4 分貝
4.1 亞歷山大·格雷厄姆·貝爾
我們前面提到過,“bel”取自于亞歷山大·格雷厄姆·貝爾的姓氏[10]。貝爾于 1874 年 3 月 3日出生于蘇格蘭愛丁堡市,1922 年 8 月 2 日逝世于加拿大新斯科舍省。在貝爾下葬那天下午 6:25,美國全國的電話線路停止服務了一分鐘,以示紀念[13]。
貝爾最被人所銘記的成就是他發明了電話。然而,他也在許多其它領域做出了非常大的貢獻。如:貝爾改進了愛迪生發明的留聲機,發明了早期金屬探測器,還與凱西·鮑德溫一同設計出了當時速度最快的水翼船 HD-1,速度達到了 30 英里每小時。貝爾也非常重視科學技術的發展,他曾是國家地理學會的主席,《國家地理》及《科學》雜志的創始人之一。
此外,貝爾還有一件非常值得稱道的是他將自己的一生奉獻給了聾啞人的教育事業。他接過并且改進了由他的父親,亞歷山大·梅爾維爾·貝爾開發的可視言語系統,這是一種用于幫助聾人學習以及提高他們語言能力的系統。著名作家海倫·凱勒就曾是貝爾的學生及摯友。也正是在這個過程中,他對人類的聽力系統進行了深入的研究。

圖源:Library and Archives Canada
亞歷山大·格雷厄姆·貝爾

圖源:National Museum of American History
貝爾的試驗型電話
4.2 分貝的歷史及定義
在電話被發明后,自然地,人們需要量化地測量任何電話系統中的聲音傳輸效率[11]。在分貝之前,人們曾使用過兩種不同的單位來衡量,自然衰減單位(The Natural Attenuation Unit)和標準電纜英里(Mile of Standard Cable)。自然衰減單位的定義是:
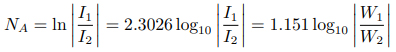
其中 I1 和 I2 流入相同的阻抗,W1 和 W2 是由 I1 和 I2 流入相同的阻抗所產生的功率[10][11]。上式的最后一步用到了在給定系統的一點: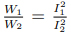 ,及對數的指數性質。然而,由于自然衰減單位的尺寸不方便,人們更常使用另一單位,標準電纜英里[11]。標準電纜的定義為:阻值為 88 歐姆/英里的 19 股開線電纜,電容為 0.054 微法/英里[7]。標準電纜英里的定義為:
,及對數的指數性質。然而,由于自然衰減單位的尺寸不方便,人們更常使用另一單位,標準電纜英里[11]。標準電纜的定義為:阻值為 88 歐姆/英里的 19 股開線電纜,電容為 0.054 微法/英里[7]。標準電纜英里的定義為:
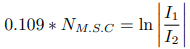
或
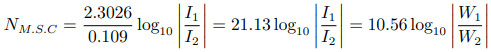
通過與自然衰減單位的對比,我們知道 1 標準電纜英里約等于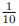 自然衰減單位[11]。這可能會讓人有些困惑,我們可以通過一張圖片來描述。
自然衰減單位[11]。這可能會讓人有些困惑,我們可以通過一張圖片來描述。
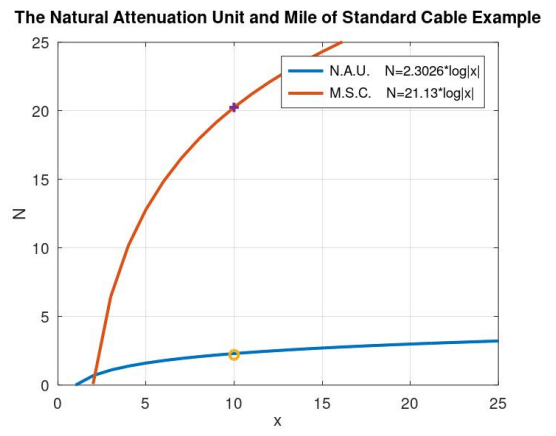
可以看到,當假設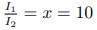 的時候,我們得到了約 2 自然衰減單位和約 20 標準電纜英里。我們也可以說,標準電纜英里相較于自然衰減單位可以反映出更細微的變化。
的時候,我們得到了約 2 自然衰減單位和約 20 標準電纜英里。我們也可以說,標準電纜英里相較于自然衰減單位可以反映出更細微的變化。
由于標準電纜的衰減常數隨頻率變化而變化,且使用 796.4 周期(ω = 5000)的頻率沒有得到普遍認可,人們采用了一個新單位,新電話傳輸單位(New Telephone Transmission Unit),并且 TU 單位有如下優點:(1) 不隨頻率變化而變化;(2) 尺度合適;(3) 具有簡單的物理意義[11]。它的定義為:
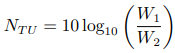
TU 的大小被選擇為與 MSC 相近。準確地說,1.0TU=0.947MSC 或 1.0MSC=1.056TU[7]。
而 TU 單位,就是分貝(dB)單位的前身!在 1928 年,貝爾實驗室將 TU 重新命名為“decibel”,即分貝。而且與我們在網上看到的消息不同,“貝爾”與“分貝”這兩個單位并不是先后被定義的,而是同時定義的。在這篇 TU Becomes Decibel 中,作者 R.V.L. Hartley 指出:因為一個乘方的對數被乘了十以得到 TU 單位,這提示 TU 天然為派生單位,則“貝爾”之名應被授予其基本單位;又因為 TU 的數值為貝爾數值的十倍,則 TU 的大小應為貝爾的十分之一,所以它將成為“分貝”[10]。
4.3 分貝的基本性質
1) 我們為什么使用分貝
簡單地講:使用分貝單位將極大簡化我們的計算!您已經了解,分貝其實就是對數運算,它的特點是可以將乘法轉換為加法、除法轉換為減法以及開根號運算轉換為除法。在對數運算被發明的最早期,它的目的就是為了減輕當時科學家們計算的難度。最初的對數以對數表的形式出現,您可以將它理解為原始的計算器。
在這里,我們引入幾個便于我們日常理解和運算的分貝數:1dB、3dB 和 10dB。我們說:±1dB對應增加或減少 26% 的增益;+3dB 增益為增加一倍功率,-3dB 為增益降低到原來的一半;+10dB 的增益需要十倍的功率,-10dB 的變化意味著將原始值降低到 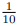 。在聲學領域,由于人體對刺激感知的特點,+10dB 的變化在經驗中被定義為大多數人認為“兩倍音量大小”的值,所以,假如您想要讓家中耳機或音響的聲音大一倍,您將需要十倍的功率!也就是提升 10dB 的功率。以此類推,如果我們需要輸出功率增加 20dB,則需要一百倍的功率!我們通過一個小推導來支持這個結論。以 +3dB 為增加一倍功率為例,假設我們正在計算的某一輸出為
。在聲學領域,由于人體對刺激感知的特點,+10dB 的變化在經驗中被定義為大多數人認為“兩倍音量大小”的值,所以,假如您想要讓家中耳機或音響的聲音大一倍,您將需要十倍的功率!也就是提升 10dB 的功率。以此類推,如果我們需要輸出功率增加 20dB,則需要一百倍的功率!我們通過一個小推導來支持這個結論。以 +3dB 為增加一倍功率為例,假設我們正在計算的某一輸出為
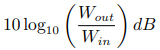
將輸出功率增加一倍,我們會得到
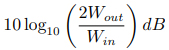
根據對數的乘法性質,上式將等于
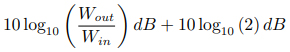
這時,如果將上式第二項輸入計算器,我們將會得到 3.01029995664,即大約 3dB。余下的推論將類似。也就是說,假如我們有兩個分別為 60dB 的功率放大器,那么它們一起輸出時的總功率將會是約 63dB,而不是 120dB。
又假設我們有一串聯放大器系統,其增益分別為 10dB,6dB,1dB,總增益為 17dB。假如
我們使用公式計算,根據分貝瓦的公式
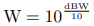
假設輸入為 1W 時,我們得到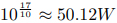 。但是,計算這樣的冪指數略顯不便。而當我們利用分貝的性質時,只需要將其分成 10dB + 3dB + 3dB + 1dB,對應的放大的倍數為 10倍,2 倍,2 倍和 1.26 倍。代入 1W 的輸入,輸出約為 1W ∗ 10 ∗ 2 ∗ 2 ∗ 1.26 = 50.4W。可見兩者非常的接近。這就是在工程實踐中,分貝單位能夠帶來的便捷性,可以讓我們更簡單地進行運算。
。但是,計算這樣的冪指數略顯不便。而當我們利用分貝的性質時,只需要將其分成 10dB + 3dB + 3dB + 1dB,對應的放大的倍數為 10倍,2 倍,2 倍和 1.26 倍。代入 1W 的輸入,輸出約為 1W ∗ 10 ∗ 2 ∗ 2 ∗ 1.26 = 50.4W。可見兩者非常的接近。這就是在工程實踐中,分貝單位能夠帶來的便捷性,可以讓我們更簡單地進行運算。
2) 分貝的簡單估算
在某些時刻,我們可能需要快速地估算某些系統的增益,這時精度相對不那么重要。我們需要記住如下三個等式:
10 log10(2) ≈ 3.01029996
10 log10(3) ≈ 4.77121255
10 log10(5) ≈ 6.98970004
這樣,我們就可以進行估算了。例如,設我們有一系統,它的增益為
10 log10(15)dB
則根據對數的乘法運算性質,它也等于
10 log10(3 ∗ 5)dB = 10 log10(3)dB + 10 log10(5)dB
即該系統增益約等于 4.8 + 7.0 = 11.8dB。我們將 10 log10(15) 輸入計算器驗算,得出的結果約等于 11.76091259。再舉一個小例子,假如我們的系統輸出為
10 log10(7)dB
這時我們可以將它估算為
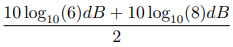
我們計算的結果約為 8.41dB,而 10 log10(7) ≈ 8.45dB。
有了上面三個基本的對數等式,我們可以快速估算出幾乎所有系統的分貝輸出。
3) 分貝自身是無量綱量
在物理學中,分為有量綱量與無量綱量兩種量。一類物理量的大小與度量時所選用的單位有關,稱之為有量綱量,例如長度、時間、質量、速度、加速度、力、動能、功等就是常見的有量綱量;另一類物理量的大小與度量時所選用的單位無關,則稱之為無量綱量,例如角度、兩個長度之比、兩個時間之比、兩個能量之比等[16]。具體到分貝單位,當它僅作為 dB 時,是一個無量綱量,因為它僅僅是兩個功率或電流的比值的對數,與度量時所選的單位無關;而當分貝加入后綴時,例如 dBW,這時它就成為了有量綱量,因為現在它以 1W 作為參考單位。
4.4 常見的分貝單位
分貝也被應用于多種不同的學科與領域,我們在這里簡單介紹幾種。它們是:
1) dBm 與 dBW
分貝毫瓦與分貝瓦是一種電平單位,用來表示功率電平相對于毫瓦或瓦的分貝。分貝毫瓦的定義為
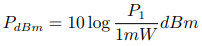
其中 P1 被標準化至 1 毫瓦[15]。我們也可以通過對數的性質推出,若要將任意 dBm 表示為毫瓦,所使用的公式為
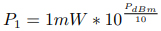
分貝瓦與分貝毫瓦類似,只不過使用 1W 而不是 1mW 作為參考。在電話與音頻電路中,0.775V 信號電平施加于 600? 的電阻產生 1 毫瓦的功率[3],而在射頻電路系統中,電阻的參考值為 50?[4]。
2) dBu 與 dBV
dBu 和 dBV 都是專門用于測量電壓的分貝單位。其中,dBu 是相對于 0.775V 的 dB 單位;dBV 是相對于 1V 的 dB 單位,于是我們有:0dBu = 0.775V ,0dBV = 1V ,并且 dBu 始終等于 dBV + 2.21[2]。其它與 dBu 和 dBV 有關的公式有[8]:
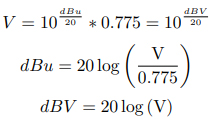
需要注意的是,dBV 的 V 應始終大寫,以便于同 dBu 區分。
3) dBi 與 dBd
dBi 或 dB(isotropic) 的定義為天線的增益與理論各向同性天線的增益的比較,理論各向同性天線在所有方向上均勻分布能量;dBd 或 dB(dipole) 的定義則為天線增益與半波偶極子天線增益的比較。dBi 的公式為
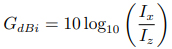
Ix 為定向天線的電磁強度,Iz 為各向同性天線的電磁強度[14]。上式也可表達為
GdBi = 10 log10 (G)
G 為天線的增益因子。然而,我們無法真正制造出理論的各向同性天線,所以人們也將簡單且效率極高的半波偶極子天線作為參考對象,即 dBd。由于半波偶極子天線的定向增益為1.64,則它的公式為
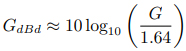
通常來講,
GdBd ≈ GdBi - 2.15dB
這兩種單位都經常被使用,需要注意的是:當指定了天線增益單位為 dBi 或 dBd 時,一般不會產生歧義。而如果僅指定了天線增益單位為 dB,則需要進一步參考資料。
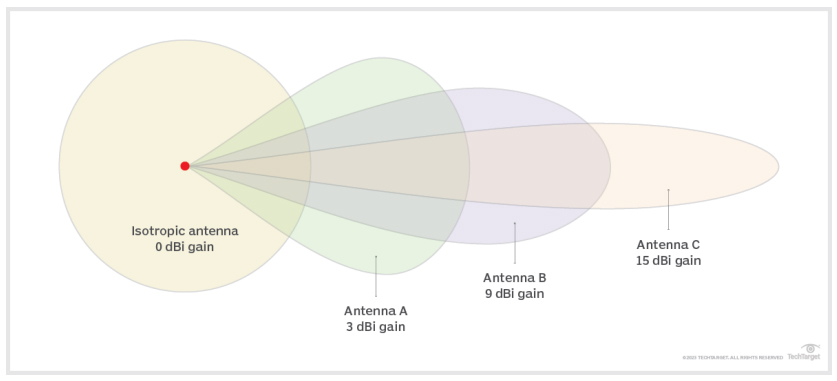
圖源:TechTarget
不同的 dBi 增益

圖源:Tele-Tech Magazine
飛機高度計的半波偶極子天線
4) dBc
dBc 或 decibel relative to carrier 的定義為信號與載波信號的功率比。如令 Psignal 為某調制信號功率,Pcarrier 為未調制載波信號功率,則瞬時調制信號信號的強度為
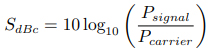
若 SdBc 為正,信號強度大于載波信號強度;反之若 SdBc 為負,則信號強度小于載波信號強度[5]。
5) dBsm
又稱 dB (m2),相較于一平方米的分貝單位,常用在雷達散射截面(Radar Cross Section,RCS)測試與天線有效面積的測試中。

圖源:Lockheed Martin
F-117 進行 RCS 測試
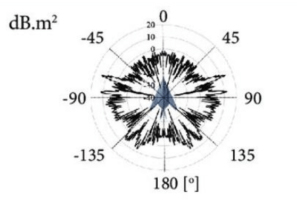
圖源:Calculation of Aircraft Target’s Single-Pulse Detection Probability[17]
F-117 的 RCS 測試結果
6) dB SPL
聲壓級是我們形容聲音大小的單位,也是日常最多接觸到的分貝單位。例如安靜的房間約為30dB、正常說話的聲音約為 60dB、飛機起飛時約 140dB。聲壓級的定義為
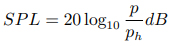
其中 ph 為參考聲壓級,即在 1kHz 時為 2∗10−5P a[1],通常被認為是人類聽力的閾值。
5 結語
希望經過本文的介紹,您已經大致了解了對數與分貝的概念,它們在我們身邊的應用遠超我們的想象。希望與您共勉,一起探索廣袤的知識海洋。
References
[1] Keith Attenborough and Michiel Postema. A pocket-sized introduction to acoustics. Postema,2008, pp. 25-26.
[2] Biamp. GAIN structure: Input and output levels. July 2023. url: https://support.biamp.com/General/Audio/Gain_structure%3A_input_and_output_levels.
[3] Stephen J. Bigelow, Joseph J. Carr, and Steve Winder. Understanding Telephone Electronics. Newnes, 2001, p. 16.
[4] Joseph J. Carr. RF components and circuits. Elsevier u.a., 2005, pp. 45–46.
[5] TechTarget Contributor. What is decibels relative to Carrier (DBC)?: Definition from TechTarget. Mar. 2011. url: https : / / www . techtarget . com / whatis / definition /decibels-relative-to-carrier-dBc.
[6] John H. Conway. Book of numbers. Springer, 2012, p. 249.
[7] Don Davis and Carolyn Davis. Sound system engineering. Sams, 1987, pp. 35–37.
[8] dB to Volts. 2023. url: https://www.extron.com/calculators/db-to-volts/?tab=tools.
[9] Douglas Downing. Algebra, the easy way. Barron’s, 2003, p. 275.
[10] R.V.L Hartley. “”TU” Becomes ”Decibel””. In: Bell Laboratories Record (December, 1928),pp. 137–139.
[11] Kenneth Simonds Johnson. Transmission circuits for Telephonic Communication: Methodsof analysis and Design. Van Nostrand co., 1925, pp. 9–12.
[12] E.R. Kandel. Principles of Neural Science, Fifth Edition. McGraw-Hill’s AccessMedicine.McGraw-Hill Education, 2013, p. 451. isbn: 9780071390118.
[13] Naomi E. Pasachoff. Alexander Graham Bell: Making connections (oxford portraits in science). Oxford University Press, 1996, p. 130.
[14] Robert Sheldon. What is decibels relative to isotropic (DBI)? Feb. 2023. url: https ://www.techtarget.com/whatis /definition/decibels- relative- to- isotropic-radiator-dBi.
[15] Robert Sobot. Wireless Communication Electronics: Introduction to RF circuits and designtechniques. Springer International Publishing, 2021, p. 252.
[16] Qingming Tan. Liang Gang Fen Xi. Zhong guo ke xue ji shu da xue chu ban she, 2005, p. 3.[17] Kuizhi Yue, Shichun Chen, and Changyong Shu. “Calculation of Aircraft Target’s Single-Pulse Detection Probability”. In: Journal of Aerospace Technology and Management 7.3(July 2015), pp. 314–322. issn: 2175-9146. doi: 10.5028/jatm.v7i3.470. url: https://doi.org/10.5028/jatm.v7i3.470.

 粵公網安備 44030902003195號
粵公網安備 44030902003195號