(3)轉發干擾時進行相位調制比較簡單。現代雷達的工作體制已從簡單的脈沖制雷達發展到脈沖多普勒(PD)和脈壓等全相參雷達，移頻干擾和調相干擾是對這種相參雷達常用的有效干擾方式。幅度量化DRFM常用的一種調制方式如圖2(a)所示。

 

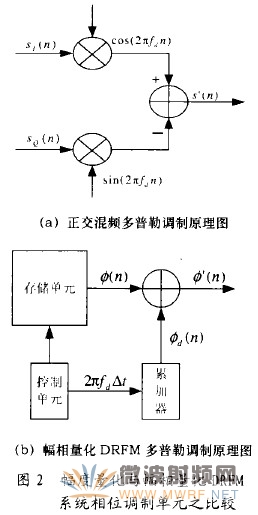
其多普勒調制器采用數字正交混頻方案。假設幅度采樣后雷達信號為

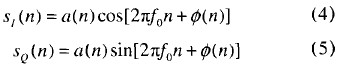
利用DDS產生cos(2πf_dn)和sin(2πf_dn)的數字信號，分別乘以同相分量S_I(n)和正交分量S_Q(n)，然后兩路數字信號相減得到：

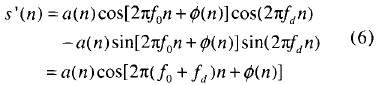
這樣S’(n)相對于原始信號有了一個多普勒頻移f_d。由以上分析可知，幅度量化DRFM在進行相位調制時每個采樣點要進行2次乘法運算和1次加法運算，運算量比較大，對于實時性要求較高的應用場合，難以滿足要求。圖2(b)是基于幅相量化DRFM的多普勒頻移干擾產生單元。控制單元以周期T_s(ADC采用周期)從存儲單元中取出相位數據流ø(n)，并按要求產生頻移常數因子2πf_dT_s送入累加器。累加器以為周期對頻移因子進行累加運算，并輸出對應的相位偏移量ø_d（n）=n·2πf_dT_s，精度取決于相位量化位數B。再經加法器與取出的雷達相位信號相加得到干擾信號的相位數據流

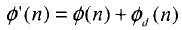
送入相幅轉換器中。通過簡單計算可知干擾信號的瞬時角頻率

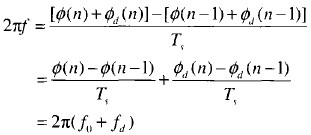
即完成了多普勒頻移調制。由于采用正交調制技術，多普勒頻移的無模糊帶寬與ADC帶寬相同，可達l／T_s。觀察圖2(b)，不難看出基于幅相量化的DRFM進行多普勒移頻干擾每個采樣點只需2次加法運算，與幅度量化DRFM相比大大減少了運算量，從而提高了處理速度。

與傳統的相位量化DRFM相比，幅相量化DRFM最顯著的優勢在于其復制信號有較高的保真度。以常用的3bit相位量化為例，理想情況下其由量化引起的寄生信號最大功率出現在7次諧波處，約為一16．9dB，難以滿足干擾PD雷達所需的寄生信號功率小于一20～-30dB的要求。當增加量化位數后，其信噪比提高不明顯，且系統復雜程度大幅度提高。幅相量化DRFM，由于其前端采用A/D幅度采樣，所以其存儲信號的保真度與使用同性能ADC的幅度量化DRFM相同，由量化噪聲引起的信噪比(S/n)_q與量化位數b的關系近似為：

(S/n)q≈6.02×b+1.76dB (9)

當A／D量化位數b=3時，即可獲得比較滿意的信噪比。而且隨量化位數的增加，信噪比呈線性提高。

4、系統仿真

筆者利用Matlab軟件的Simulink工具箱，對這種基于幅相量化的DRFM系統進行建模與仿真。模擬雷達射頻信號為20MHz單頻正弦波，系統前端采用正交AD采樣，本振頻率f_o=21MHz，經混頻、低通濾波后的中頻頻率f_o=21—20=1MHz，量化位數b=8，采樣頻率f_o=4MHz。，I，Q數字信號經幅相轉換器變換，輸出一路相位數據，存入存儲器中，存儲長度為0．1ms。轉發過程與儲頻過程相反，前面已經討論，這里不再敷述。

由于在未加干擾時同比特幅相量化與幅度量化DRFM的信號保真度相同，而幅度量化與相位量化DRFM的保真度比較，參考資料4中已做了詳細的論證和仿真，所以本文重點對同比特幅度量化與幅相量化DRFM對脈內幅度起伏信號的復制效果做一仿真比較。