文章里講解了關于射頻IQ調制器、零中頻架構相關的原理及技術，全都是干貨！其實好多同行對軟件無線電的原理、IQ調制、鏡像抑制都是一知半解，知其然不知其所以然。好好研讀這篇文章，相信會讓你有種恍然大悟的感覺。

RF工程常被視為電子領域的黑魔法。它可能是數學和力學的某種 奇特組合，有時甚至僅僅是試錯。它讓許多優秀的工程師不得其解， 有些工程師僅了解結果而對細節毫無所知。

復數混頻器、零中頻架構和高級算法開發之間存在一種有趣的聯系。本文旨在明確以上三者各自的基本概念，即工作原理以及它們 給系統設計帶來的價值，并闡述它們之間的相互依賴關系。

RF工程常被視為電子領域的黑魔法。它可能是數學和力學的某種 奇特組合，有時甚至僅僅是試錯。它讓許多優秀的工程師不得其解， 有些工程師僅了解結果而對細節毫無所知。現有的許多文獻往往 不建立基本概念，而是直接跳躍到理論和數學解釋。

復數RF混頻器揭秘

圖1是采用上變頻器（發射機）配置的復數混頻器原理圖。兩條并 行路徑各有獨立混頻器，一個公共本振向這些路徑饋送信號，本振 與其中一個混頻器的相位相差90°。兩個獨立輸出隨后在求和放大 器中求和，產生所需的RF輸出。

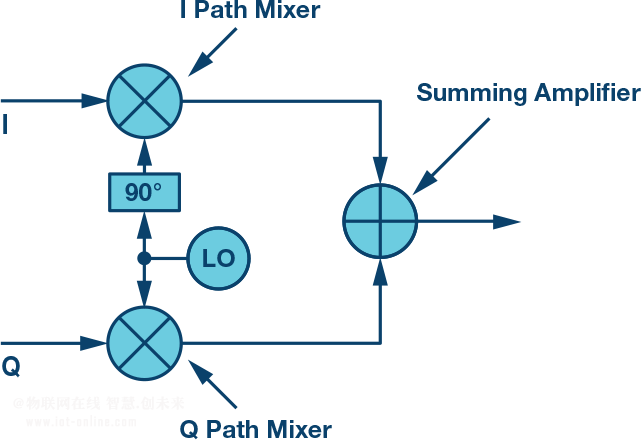
?圖1. 復數發射機基本架構

該配置有一些簡單但非常有用的應用。假設僅在I輸入上饋送一個 信號音，而不驅動Q輸入，如圖2所示。假定I輸入上的信號音頻率 為x MHz，則I路徑中的混頻器產生LO頻率±x的輸出。由于沒有信號 施加于Q輸入，此路徑中的混頻器產生的頻譜為空，I混頻器的輸出 直接成為RF輸出。

?圖2. I路徑分析

或者，假設僅向Q輸入施加一個頻率為x的信號音。Q混頻器進而產 生信號音為LO頻率±x的輸出。由于沒有信號施加于I輸入，其混頻 器輸出靜音，Q混頻器的輸出直接成為RF輸出。

?圖3. Q路徑分析

乍看起來，圖2和圖3的輸出似乎完全相同。但實際上，二者有一個 關鍵差異，那就是相位。假設將相同信號音同時施加于I和Q輸入， 并且輸入通道之間存在90°相移，如圖4所示。

?圖4. 同時施加I和Q信號的路徑分析

仔細審視混頻器輸出，我們觀察到：LO頻率加輸入頻率的信號是 同相的，但LO頻率減輸入頻率的信號是異相的。這導致LO上側的信 號音相加，而下側的信號音相消。沒有任何濾波，我們便消除了其 中一個信號音（或邊帶），產生的輸出完全位于LO頻率的一側。

在圖4所示例子中，I信號比Q信號超前90°。如果變更配置使得Q信 號比I信號超前90°，那么可以預期會有類似的相加和相消，但在這 種情況下，所有信號將出現在LO的下側。

?圖5. 信號音位置取決于I和Q的相位關系

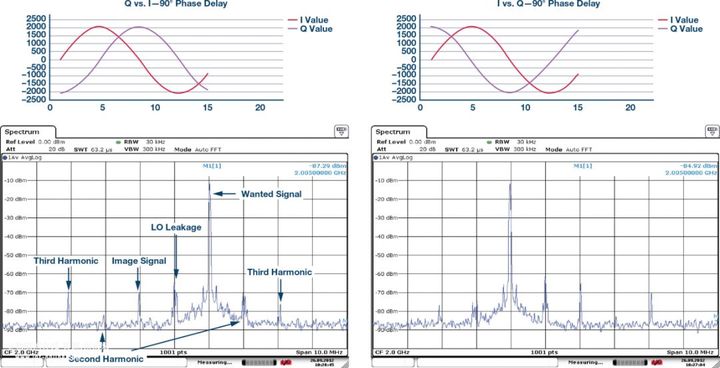
上面的圖5顯示了一個復數發射機的實驗室測量結果。左邊顯示的 是I比Q超前90°的測試案例，其導致輸出信號音位于LO的上側。圖5 右邊顯示了相反的關系，即Q比I超前90°，由此得到的輸出信號音位 于LO下側。

理論上應當可以讓全部能量僅落在LO的一側。然而，如圖5中的實 驗室測量結果所示，在實踐中完全相消是不可能發生的，有一些 能量會留在LO的另一側，這就是所謂鏡像。還應注意，LO頻率的 能量也是存在的，稱為LO泄漏或LOL。結果中還可以看到其他能 量—這些是所需信號的諧波，本文不予以討論。

為了完全消除鏡像，I和Q混頻器輸出的幅度必須完全一致，而在LO 鏡像側上彼此之間的相位恰好相差180°。如果不能滿足上述相位 和幅度要求，那么圖4所示的相加/相消過程就會不太理想，鏡像頻 率的能量仍會存在。

影響

采用常規單混頻器架構時，產生LO±產物。發射之前需要消除其中 一個邊帶，通常是通過增加帶通濾波器來消除。濾波器的滾降頻 率必須適當，使其既能消除不需要的鏡像信號，又不會影響需要 的信號。

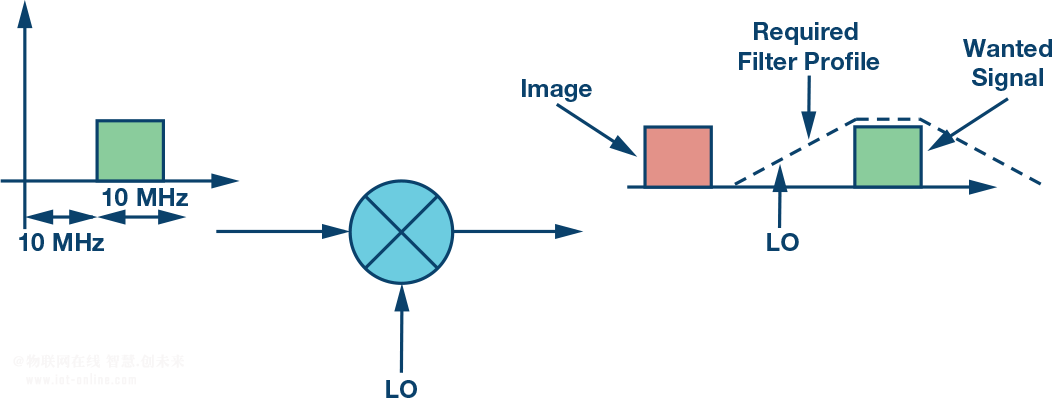
?圖6.單混頻器鏡像濾波器要求

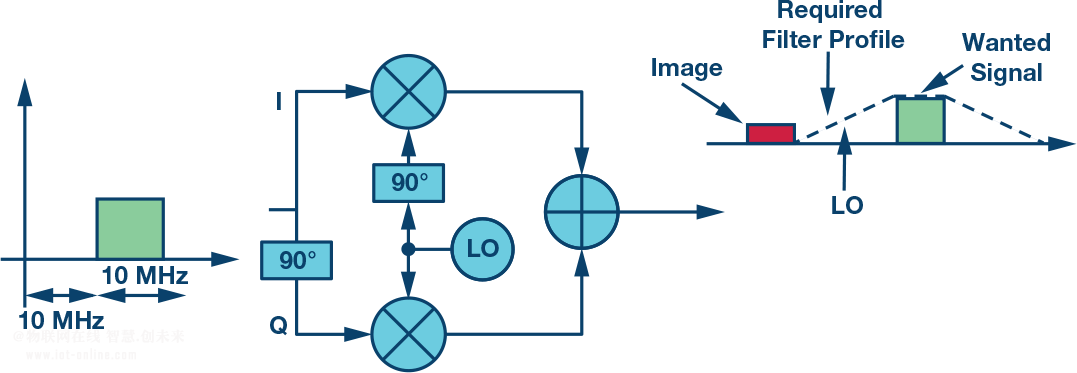
鏡像和所需信號之間的間隔會直接影響到對濾波器的要求。如果間隔較大，可以使用滾降較緩的簡單低成本濾波器。如果間隔較窄，設計必須實現具有陡峭響應的濾波器，通常采用多極點或SAW濾波器。因此可以說，鏡像和所需信號之間必須保持適當的間隔，以便可以濾除鏡像而不影響所需信號；該間隔與濾波器的復雜度和成本成反比。此外，如果LO頻率可變，濾波器必須可調諧，這會進一步增加濾波器的復雜度。

鏡像和所需信號之間的間隔由施加于混頻器的信號決定。圖6中的例子顯示一個與DC相距10 MHz的10 MHz帶寬信號。相應的混頻器輸出將鏡像置于與所需信號相距20 MHz的地方。這種配置中，為在輸出端實現10 MHz的所需信號頻譜，必須讓一條20 MHz基帶信號路徑連接到混頻器。10 MHz的基帶帶寬未使用，混頻器電路的數據接口速率高于必要水平。

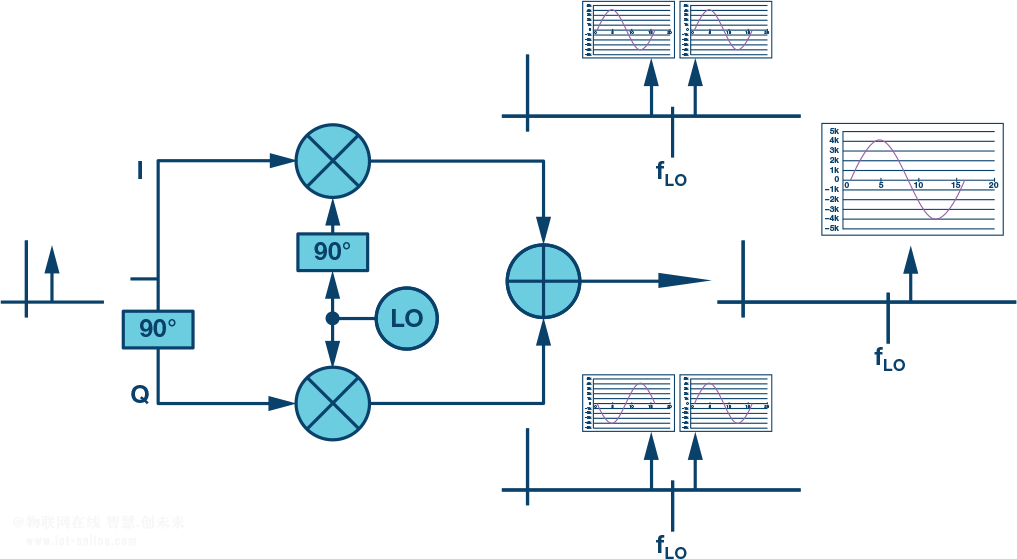
回到圖5所示的復數混頻器，我們知道其架構消除了鏡像而無需外部濾波。而且，在零中頻架構中可以優化效率，使得信號路徑處理帶寬等于所需信號帶寬。圖7所示的概念圖說明了其實現原理。如上所述，如果I比Q超前90°，則僅LO上側會有輸出。如果Q比I超前90°，則僅LO下側會有輸出。因此，如果產生兩個獨立基帶信號，其中一個設計成僅產生上邊帶輸出，另一個設計成僅產生下邊帶另一個設計成僅產生下邊帶輸出，那么可以在基帶中將其相加并施加于復數發射機。結果將是具有不同信號的輸出出現在LO上側和下側。在實際應用中，組合基帶信號以數字方式產生。圖7所示求和節點僅是為了說明此概念。

?圖7.零中頻復數混頻器架構

零中頻紅利

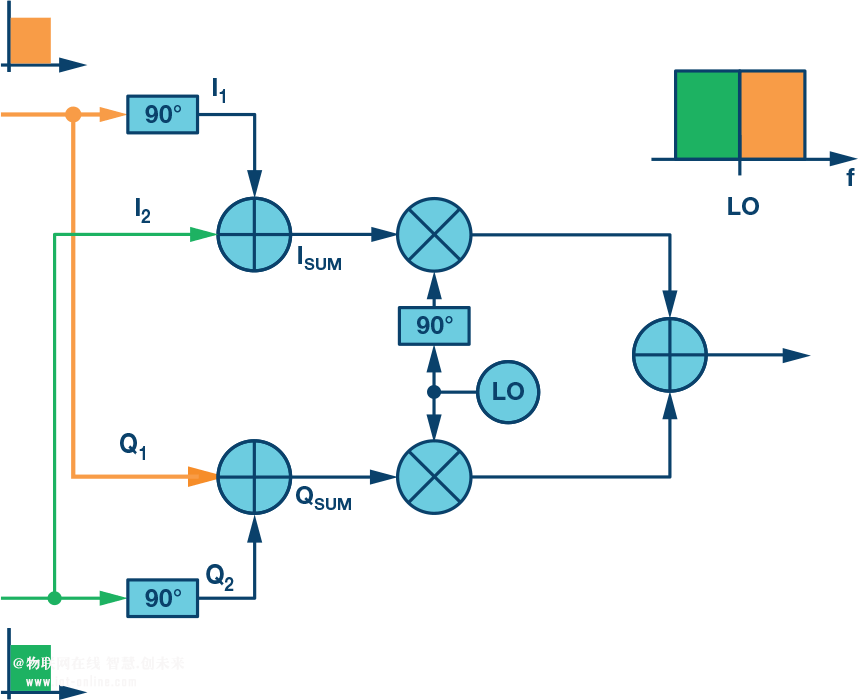
利用復數發射機產生單邊帶輸出具有相當大的好處，可減少為消除鏡像所需要的RF濾波。然而，如果鏡像相消性能足夠好，使得鏡像可忽略不計，那么可以使用零中頻模式來進一步發揮該架構的優勢。零中頻允許我們使用特別創建的基帶數據來產生RF輸出，從而在LO兩側出現相互獨立的信號。圖8顯示了這是如何實現的。我們有兩組相互獨立的I和Q數據，用符號數據編碼，接收機可以根據基準載波的相位進行解碼。

?圖8.深入考察零中頻復數混頻器配置中的I/Q信號

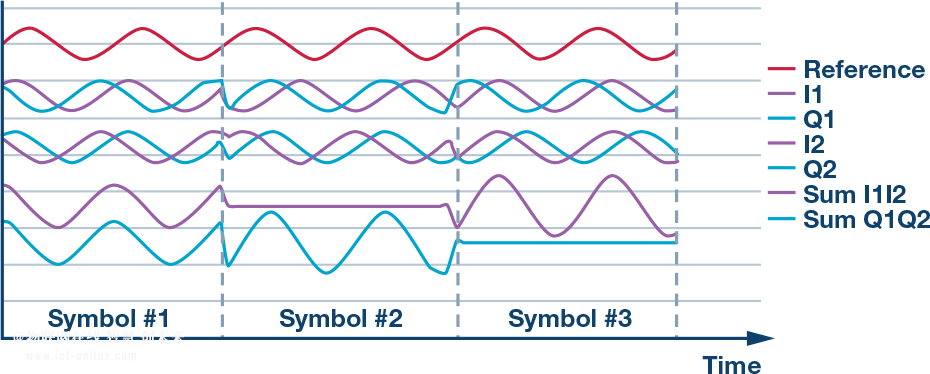
初始觀測顯示：Q1比I1超前90°，二者的幅度一致。類似地，I2比Q2超前90°，其幅度同樣一致。將這些獨立信號合并，使得I1 + I2 = SumI1I2，Q1 + Q2 = SumQ1Q2。相加后的I和Q信號不再表現出相位和幅度相關性—其幅度在所有時候都不相等，二者之間的相位關系不斷變化。所得的混頻器輸出將I1/Q1數據置于載波的一側，將I2/Q2數據置于載波的另一側，如上所述及圖7所示。

通過將彼此相鄰的獨立數據塊置于LO的任一側，零中頻使復數發射機的優勢得到加強。數據處理路徑帶寬絕不會超過數據帶寬。因此，理論上，在零中頻架構中使用復數混頻器便提供了一種解決方案，其不需要RF濾波，同時還能優化基帶功率效率，降低不可使用信號帶寬的單位成本。

到目前為止，本文的重點是復數混頻器用作零中頻發射機。同樣的原理反過來也成立，即復數混頻器架構可以用作零中頻接收機。針對發射機說明的優勢同樣適用于接收機。使用單混頻器接收信號時，首先必須利用RF混頻器濾除鏡像頻率。在零中頻工作模式下，無需擔心鏡像頻率，高于LO的信號接收與低于LO的信號接收是相互獨立的。

復數接收機如下圖所示。輸入頻譜同時施加于I和Q混頻器。一個混頻器通過LO驅動，另一個混頻器通過LO + 90°驅動。接收機的輸出為I和Q。對于接收機來說，要想由經驗證明給定輸入對應的輸出將會如何并不容易，但如果輸入信號音高于LO，如圖所示，那么I和Q輸出將處于(信號音 – LO)頻率，并且I和Q之間會有相移（I比Q超前）。類似地，如果輸入信號音低于LO，那么I和Q輸出同樣是在(LO – 信號音)頻率，但這時是Q比I超前。通過這種方式，復數接收機可以區分高于LO的能量和低于LO的能量。

復數接收機的輸出將是兩種I/Q信息之和：一種代表接收到的高于LO的頻譜，另一種代表接收到的低于LO的頻譜。這一概念已在前面針對復數發射機做過說明，其中是將相加后的I信號和相加后的Q信號施加于復數發射機。對于復數接收機，接收相加后的I信息和相加后的Q信息的基帶處理器可利用復數FFT來輕松區分較高頻率和較低頻率。

?圖9.零中頻復數混頻器接收機配置

收到相加后的I信號和相加后的Q信號時，有兩個已知量——相加后的I信號和相加后的Q信號——但有四個未知量，即I1、Q1、I2和Q2。由于未知量多于已知量，因此似乎無法解出I1、Q1、I2和Q2。然而，我們還知道I1 = Q1 + 90，I2 = Q2 – 90，有了這兩個已知關系后，便可利用收到的相加后的I信號和相加后的Q信號解出I1、Q1、I2和Q2。事實上，我們只需解出I1和I2，因為Q信號是I信號的副本，不過相位偏移±90而已。 限制

實踐中，復數混頻器試圖完全消除鏡像信號。這一限制對無線電架構設計有兩個突出影響。

即使有性能限制，復中頻仍能帶來切實的好處。試考慮圖10所示的低中頻例子。由于性能限制，我們確實能看到鏡像。然而，同對單混頻器設計的預期相比（參見圖6），該鏡像已大為衰減。雖然復數混頻器仍需要濾波器，但對該濾波器的要求可以放松很多，其實現也較簡單，成本較低。

?圖10.復數混頻器的實際實現注意衰減的鏡像

濾波器復雜度與鏡像和所需信號之間的距離成反比。如果使用零中頻配置，該距離將變為0，鏡像位于所需信號頻段中。零中頻理論的實際應用無法完全實現，產生的帶內鏡像導致性能降低到不可接受的水平（參見圖11）。

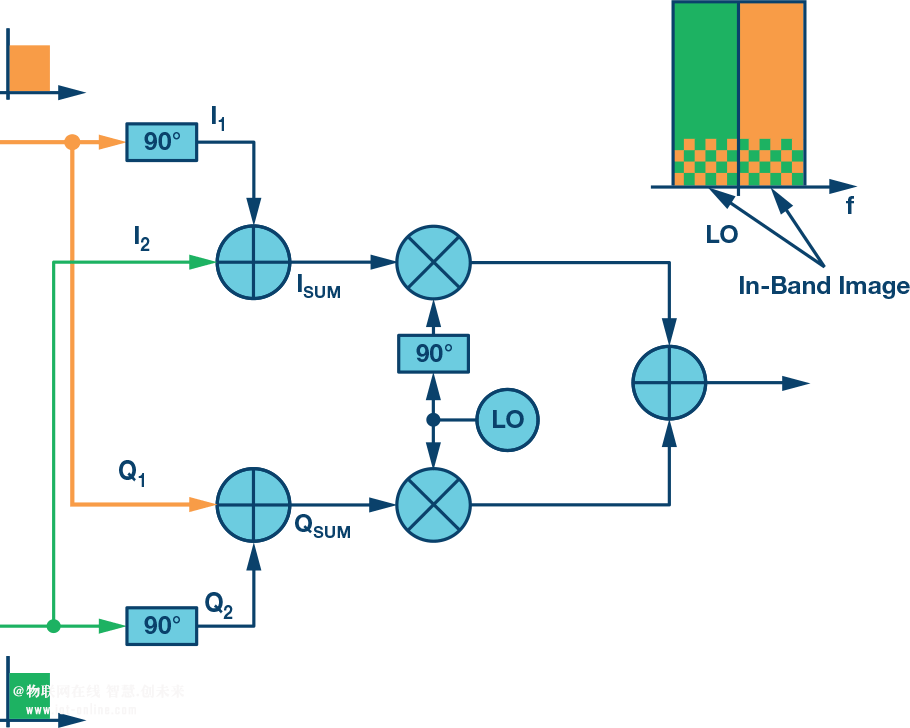
?圖11.零中頻實現的限制

只有滿足I和Q數據路徑的相位和幅度要求，復數發射機和接收機的原理才成立。信號路徑的不匹配會導致LO兩側的鏡像信號不能精確相消。此類問題的例子參見圖10和圖11。在不使用零中頻的情況下，可以采用濾波來消除鏡像。然而，若使用零中頻架構，不需要的鏡像會直接落在所需信號的頻譜范圍內，如果鏡像功率足夠大，就會發生故障狀況。因此，只有設計能消除信號路徑上的相位和幅度不一致時，使用零中頻和復數混頻才能提供最優系統設計方案。

高級算法支持

復數混頻器架構的概念已存在很多年，但在動態無線電環境中滿足相位和幅度要求的挑戰限制了其在零中頻模式下的使用。ADI公司綜合運用智能硅片設計和高級算法，克服了這些挑戰。設計允許存在影響信號路徑的因素，但智能硅片設計將這些影響降至最低。剩下的誤差通過自優化正交糾錯(QEC)算法消除。圖12是概念圖。

?圖12.高級QEC算法和智能硅片設計支持零中頻架構

在AD9371等收發器上，QEC算法位于片內ARM®處理器中。它持續掌握硅片信號路徑、經調制的RF輸出、輸入信號和外部系統環境的信息，并利用此信息以受控的預測方式智能適應信號路徑輪廓，而不是做出本能式被動反應。該算法性能出色，可將其視為以數字方式輔助模擬信號路徑發揮最佳性能。

收發器內部有多種高級算法駐留并發揮作用，動態QEC校準算法只是其中一個較突出的例子。其他與之共存的算法還有LO泄漏消除等，這些算法將零中頻架構的性能提升到最優水平。此類第一代收發器算法主要用于支持實現相關技術，而第二代算法（例如數字預失真或DPD）不僅能增強收發器的性能，還能提升整個系統的性能。

所有系統都有一些不足之處會限制其性能。第一代算法主要聚焦于通過校準消除片內限制，而新一代算法則利用智能手段來消除收發器外部的系統性能和效率限制因素，例如PA失真和效率（DPD和CFR）、雙工器性能(TxNc)、無源交調問題(PIM)等。

結語

復數混頻器已存在很多年，但其鏡像抑制性能不允許將其用于零中頻模式。智能硅片設計和高級算法的結合消除了原先阻止高性能系統采用零中頻架構的性能障礙。性能限制消除之后，采用零中頻架構對降低濾波、功耗、系統復雜度、尺寸、熱量和重量都有好處。

對于復數混頻器和零中頻，我們可以考慮將QEC和LOL算法用作支持功能。但是，隨著算法開發范圍的擴展，它給系統設計人員帶來了更高的性能水平，使他們能更靈活地設計無線電。他們既可選擇增強的性能，也可利用算法提供的助益來減少無線電設計的成本或器件尺寸。

作者：ADI Dave Frizelle,Frank Kearney