在濾波器魔法師之12(使用“Million Monkeys”提供的方法設計濾波器)中，我給自己安排了一項額外的工作，即在我匆匆完成那篇行文迅速、引人入勝的文章時，我曾允諾對各種濾波器設計和網絡理論問題進行深入探討。本文就是這些“深潛”系列(不好意思，我們公司的行話)的開篇之作：我為何把源電阻和負載電阻設置為相同的值?

　　本文使用的濾波器拓撲結構為雙端接LC梯式濾波器。由電感器和電容器構成的網絡有兩個“端口”，供信號進入和離開網絡。在我們的濾波器中，輸入端口從具有特定電阻值的信源處獲得信號(一般無法變更)，輸出端口則連接到由另一個電阻構成的“負載”(通常可以加以控制)。

　　圖1顯示的是示例濾波器。它與前文所述的網絡一致，輸出端采用與信源電阻值一樣的電阻端接。圖2顯示的是非常良好且平坦的通帶響應。圖3顯示的是去掉端接電阻后的較差響應。　　

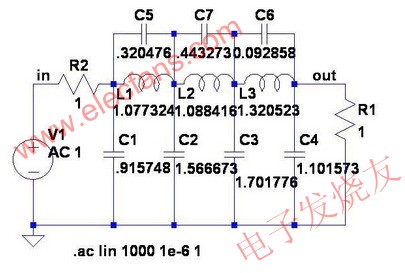
圖1: 雙端接低通濾波器示例　　

圖2：圖1器件在具有負載電阻值情況下的電壓增益　　

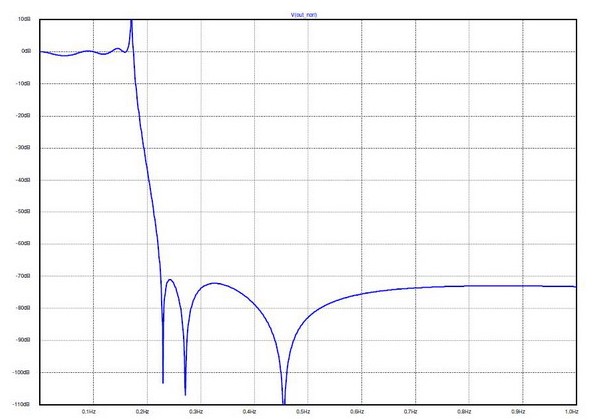
圖3：圖1器件在無負載電阻值情況下的電壓增益

　　我們可以看到，對于本文所用的特定元器件值，低漣波平坦響應只有在我們加入負載電阻的情況下才會出現。但這并非是具有兩個電阻的結果。圖4是在無負載電阻情況下產生同等振幅響應(圖5)的網絡值集合。其電壓增益為0dB，而非6dB。你是否真的愿意在大多數實際情況中使用該濾波器?答案不言而喻，因為響應相同，而增益更大，且可以節省一個元件，誰不喜歡呢?　　

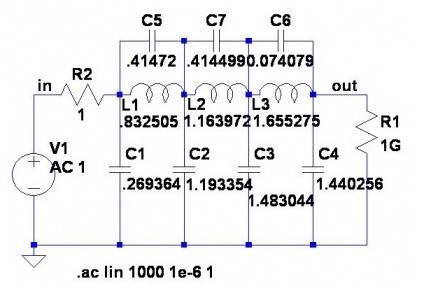
圖4：無負載電阻情況下的各元器件值組合　　

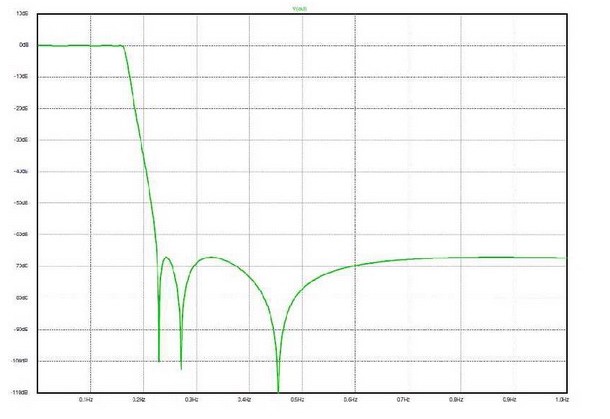
圖5：沒有負載電阻，響應依舊非常出色且平坦

　　圖6和圖7說明了我們抗拒采用“單端接”誘惑的原因。兩圖是元件值在±5%允許范圍內變化時，100個響應曲線疊加在一起的狀況。我們可以清晰直觀地看出雙端接濾波器更能夠適應所使用組件值的小幅度變化。我們在下文中還可以看到當我們使用某些擴展技巧，在不使用這些電感器的情況下以這些網絡為“原型”構建有源濾波器時，這種特性仍然得以保留。　　

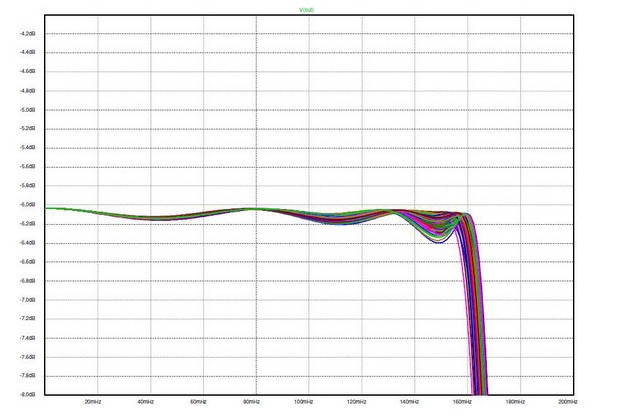
圖6：對圖1值的蒙特卡羅分析　　

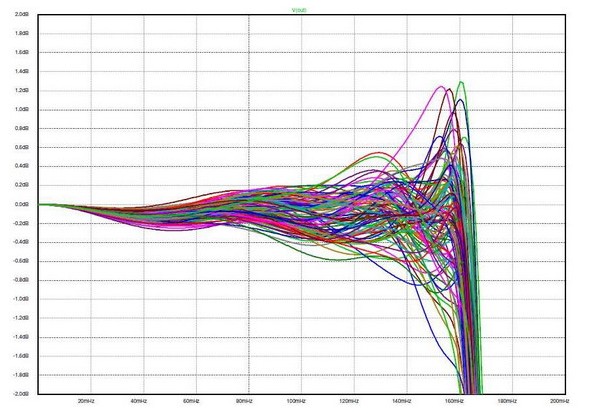
圖7：對圖4值的蒙特卡羅分析

　　雙端接濾波器有什么特別之處呢?要回答這個問題，我們需要考慮在信號從源電阻到負載電阻通過LC網絡時，發生了什么?

　　稍微岔開一下話題。想象一下你正在面試一個模擬設計崗位，并要求回答下面的問題：

　　“你有一個50歐姆輸出阻抗的正弦波發生器，輸出開路的情況下可以輸出1Vrms的電壓。客戶給你一個黑盒子，輸入阻抗為3.3K歐姆，且如果該黑盒子要正常工作，需要至少3Vrms的50KHz輸入信號。你需要讓系統工作，但沒有電源。你在實驗室唯一能夠使用的電子組件是無源兩引線組件。請說明如何解決上述問題及其工作原理。”(案例1)

　　那么這就意味著沒有電池或太陽能電池，也沒有晶體管或集成電路，而且肯定也沒有變壓器。在繼續讀下去之前(特別是你準備參加面試的情況下)好好想想。也許我們可以從圖2找到一些靈感。完成了嗎?這里有個適用的解決方案：　　

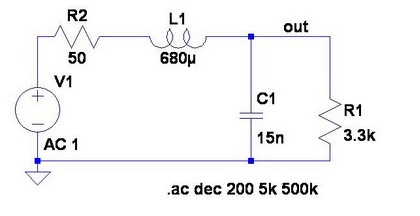
圖8：適合案例1的解決方案　　

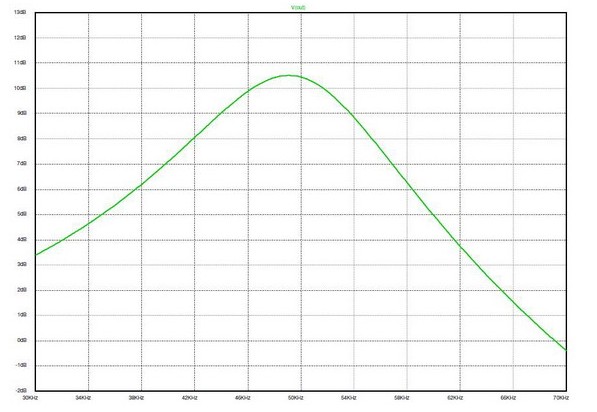
圖9：圖8解決方案的頻率響應

　　我們只使用無源兩線組件構建一個高Q值低通濾波器。圖9顯示的是信號發生器設置為開路輸出1Vrms到黑盒子電壓的全頻段狀況。我們明確無誤地實現了讓系統在規定頻率上工作的電壓增益。那么，什么地方有免費的午餐呢?

　　當然什么地方都不會有。我們可以問個額外的問題：“我們能夠從這類解決方案得到的最大電壓增益值是多少?”要得到結果，首先要認識到，雖然從這樣的元器件組合中得到電壓增益是常見的，但不可能得到功率增益。這就是理解這些無源濾波器網絡的關鍵所在：功率進入網絡，然后離開網絡。如果信源能在特定輸出電阻上提供特定的輸出電壓，對于連接的負載而言，能夠耗散的功率有嚴格的上限。你可能在學校中學習過最大功率定理，但沒有投入太多注意。但對無源濾波器而言，這個定理非常重要，所以今后應該予以關注。

　　可能你已經記起來了，實現最大功率傳輸的條件是負載電阻和信源電阻相等。你可以使用大學里學到的枯燥無味的微積分來證明。先用一個表達式表達負載電阻上耗散的功率，根據負載電阻RL計算該功率的導數。將導數設為0，然后求解RL。繼續，就是這么計算的。

　　是不是一下子豁然開朗了?你首先想到的是用變壓器。這是讓負載電阻與信源電阻匹配的傳統方法。在理想的情況下，變壓器可以把功率從信源無損地傳輸到負載，不過它一般用于電壓、電流不同的情況下。使用適當的匝比，不論負載電阻值是多少，都可以在理想的情況下在負載電阻上獲得相同的耗散功率。

　　這就是我們對圖8的LC濾波器網絡采用的措施：我們引入了一個變壓器。所有進入LC網絡的功率又出去了。在采用適當的組件值的情況下，我們可以讓所有功率在特定的頻率上全部到達負載上，而不用管負載的值是多少。

　　如果我們可以使用變壓器或者變壓器的等效LC線路，我們可以計算出50歐姆信源和3.3K歐姆負載之間能夠獲得的最大電壓增益。需要的電壓變換等于阻抗比的平方根，在本例中為8.12倍。將該比例與我們在等電阻端接例子中的電壓增益0.5相乘。所以在任意LC值下可以得到的最大增益為4.06倍，或者大約12.2dB。圖10顯示的是用我們自制的變壓器任意選擇1,000種不同的L和C值得到的結果。響應曲線的峰值從未超過預計值。至于為什么不是每個頻率下所有功率都耗散在負載上，是因為部分功率被反射回了信源。　　

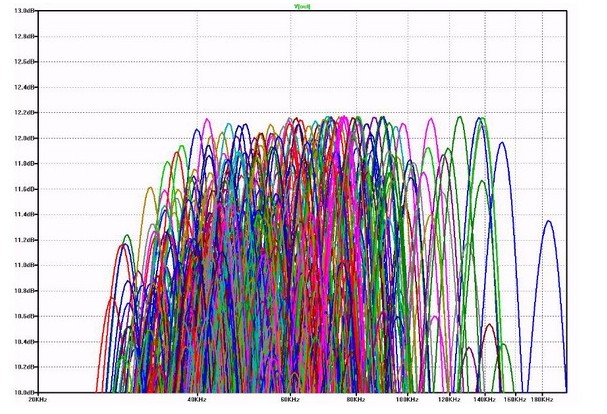
圖10：響應曲線的峰值從未超過預計值

　　所有射頻工程師都開始不耐煩地打哈欠了，因為這是你們的常識。設計LC網絡，確保讓所有信源的功率傳輸到負載，是一項稱之為阻抗匹配的核心射頻技術。這確實像兩個不等電阻之間的濾波器設計(每種設計方案都有其伴隨的虛部需要加以考慮)。一般是用L和C來完成的，而非體積龐大、成本高昂的變壓器。除微波頻段外，其中的變壓器體積不大、價格也不高，不過當導體靠得太近的時候，會造成諧振波峰。

　　現在回到我們最初討論的問題。為什么一個(設計合理的)雙端接濾波器有如此出色的“靈敏度”屬性?這是因為對濾波器通帶內的一個或者有時多個頻率，它工作在功率傳輸的最大可能點上。請再次觀察圖6和圖7。在雙端接濾波器情況下，組件值的任何變化只會讓功率傳輸(隨之為電壓增益)下降而非上升。在被稱之為反射零點的特定關鍵頻率上，濾波器響應的“靈敏度”與網絡中每個無功部分呈拋物線函數的下行段關系。這樣就很難讓網絡的響應比沒有應用功率傳輸約束的時候更差。后者狀況指的是單端接的時候，或者任何濾波器的設計響應未能滿足最大功率增益值的時候。要得到最大功率增益值，可以拋開濾波器，使用變壓比較為合適的理想變壓器。

　　還有一個問題。我們在開始的時候曾經比較過兩種濾波器，其中一種濾波器的負載電阻與信源電阻相等，另一個則沒有負載電阻。我們能否在盡可能大的給定信源電阻和負載電阻比率下成功設計出低靈敏度、等頻率響應的濾波器?有時候是可以的，但具體到我們的低通濾波器則不能。對于具體的響應，我們要求平坦的響應，讓DC增益與那些“觸點”最大值相等。這就意味著在該極低靈敏度濾波器中，信源電阻和負載電阻必須等值。對于更加普遍的情況，如果不需要對通過的0頻率或者無窮頻率施加特定的衰減，通常可以設計出任意兩個阻抗間的最低靈敏度(即理想匹配)濾波器。至于如何實現，足夠寫上幾本書，不過初學者就不用看了。