|
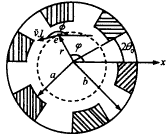
圖1 中空外開槽波導及電子注橫截面示意圖.虛圓為電子注橫截面示意圖 在Ⅰ區(0<r<a)中
在Ⅱ區(a<r<b)中 Ez=0 (4)
其中
在以上各式中,E0為高頻場振幅,Γ為角向諧波數,ΑΓ為角向Γ次諧波項的振幅系數,kc為截止波數,q為開槽序數(q=1,2,…,N),m代表高頻場的角向模式(m=0,1,2,…,N-1).AΓ的值以及電路的色散關系可由電磁場在r=a處的邊界條件確定.
色散關系為
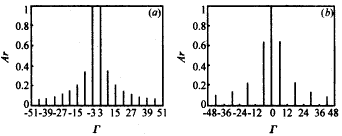
式(9)表明,只有當空間諧波次數Γ=m+lN時,非零空間諧波項才存在.角向模式決定相鄰隙間高頻場的相位差,對于每一具體模式,此相位差值為m2π/N.每一角向模式均由無數個角向諧波項組成,其諧波振幅系數由式(9)決定.在所有角向模式中有兩個比較重要的模式,即π模式和2π模式,其角向諧波相對強弱分布情況見圖2.由圖2可知,2π模式的能量主要集中于零次諧波項中,而π模式的能量主要集中于±N/2次諧波項中.因此,π模式較2π模式更適合于高次回旋諧波互作用.如果電子注回旋諧波次數(用S表示)已經設定,那么槽數N的選擇應保證最強非零次角向諧波項的次數Г與回旋諧波次數S相等.如,對于π模式,槽數N應等于2S. |
|
圖2 角向諧波振幅對角向諧波數(Γ)的相對分布示意圖.(a)π模式(m=N/2,N=6,θ0=15°),(b)2π模式(m=0,N=6,θ0=15°) 當角向模式m和槽深(即a/b的值)確定后,截止波數kc的值可由式(10)通過數值求解方法求得[6,8,9]. 三、自洽非線性理論
上述各式中,Cmn為電場歸一化系數,f(z)為一復函數,代表高頻場沿Z軸的緩變分布情況.Cmn的值由下式求得
以下是自洽非線性注波互作用常微分方程組.
以上各式中,m0和γ分別為電子的靜止質量和相對論因子,φ為動量空間角,u=γv,v為電子的速度,如圖1所示.
上式中,P為在一個高頻場周期內所取的電子注批數,M為考慮電子注厚度因數而將電子注化分的圈 |

 (1)
(1) (2)
(2)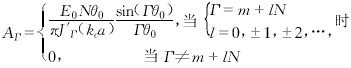 (9)
(9)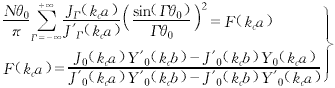 (10)
(10)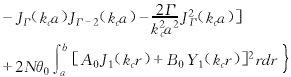 (14)
(14)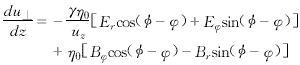 (15)
(15)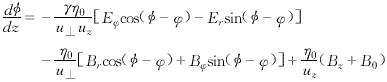 (17)
(17)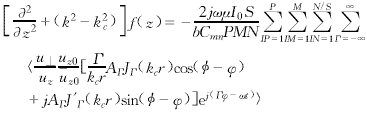 (18)
(18) 粵公網安備 44030902003195號
粵公網安備 44030902003195號