1、引言

隨著現(xiàn)代無線通信技術(shù)的飛速發(fā)展,人們對(duì)移動(dòng)通信業(yè)務(wù)的追求逐漸從單純的語音業(yè)務(wù)擴(kuò)展到多媒體業(yè)務(wù),諸如即將開始的3G業(yè)務(wù)(3rd Generation,含義為第三代數(shù)字通信[1-2])將使頻譜資源變得越來越擁擠,即通信信號(hào)帶寬隨著每代更新而逐漸加寬:從2G中的GSM200KHz到3G中的UMTS單載波5MHz,其帶寬就有25倍的增加。在IEEE 802.11n WLAN標(biāo)準(zhǔn)中,信號(hào)的發(fā)射標(biāo)準(zhǔn)更是被確定為40MHz。因此,為了節(jié)約頻譜資源,如CDMA、WCDMA等很多通信系統(tǒng)都采用頻譜利用率較高的調(diào)制方式,諸如QPSK、8PSK,M-QAM等,但隨之產(chǎn)生的問題是處理較大峰均比的非恒包絡(luò)調(diào)制信號(hào)。同時(shí)將多個(gè)載波信號(hào)組合成一個(gè)寬帶信號(hào)時(shí),亦會(huì)產(chǎn)生較大的包絡(luò)起伏,這些都對(duì)最關(guān)鍵和最昂貴器件射頻功率放大器提出了很高的線性要求。

隨著數(shù)字信號(hào)處理技術(shù)的發(fā)展,數(shù)字預(yù)失真系統(tǒng)逐漸展示出其優(yōu)越性,并且通常將其應(yīng)用于數(shù)字系統(tǒng)的基帶部分,它不僅能補(bǔ)償因功率放大器本身非線性特性的影響,同時(shí)也能對(duì)溫度濕度等環(huán)境因素進(jìn)行校正。考慮到成本較低,體積較小,國內(nèi)一些先進(jìn)的通信設(shè)備制造商已經(jīng)開始試用該技術(shù)。

而針對(duì)功率放大器線性化的數(shù)字預(yù)失真系統(tǒng)的首要前提就是必須正確而高效地估測(cè)出反饋環(huán)路延遲信息,以便于對(duì)正確補(bǔ)償功率放大器的非線性量。本文即針對(duì)反饋環(huán)路延遲估計(jì),對(duì)環(huán)路延遲估測(cè)方法對(duì)系統(tǒng)的影響進(jìn)行分析。

2、基于功放的記憶多項(xiàng)式預(yù)失真算法原理

由于無法預(yù)先獲得功率放大器的模型參數(shù),本文所涉及的多項(xiàng)式預(yù)失真系統(tǒng)采用非直接學(xué)習(xí)結(jié)構(gòu)(間接學(xué)習(xí)結(jié)構(gòu))。這種結(jié)構(gòu)具有更為穩(wěn)定的均方誤差性能和更快的收斂速度,如圖1所示:

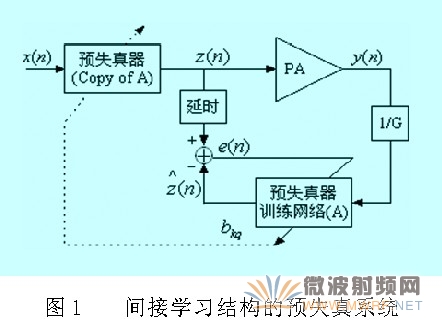
2.1、延遲估計(jì)算法原理

數(shù)字基帶自適應(yīng)預(yù)失真方法都存在著耦合反饋回路的延遲估計(jì)問題,以保證正確的基帶解調(diào)[3]。環(huán)路延遲是指信號(hào)從系統(tǒng)輸入端口到反饋輸出端口,由系統(tǒng)各器件造成的時(shí)間延遲,并且這類延遲會(huì)隨著時(shí)間和溫度而改變,因此,要不斷的調(diào)整估計(jì)結(jié)果。很多方法都有不同的優(yōu)缺點(diǎn),諸如對(duì)信號(hào)造成的畸變影響不敏感[4],對(duì)系統(tǒng)制式的限制[5],或者估計(jì)過程較復(fù)雜[6-7]。

通常對(duì)延遲估計(jì)采用數(shù)據(jù)流相關(guān)算法:
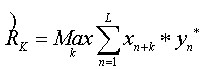        (1)
        式中,表示在環(huán)路延遲為時(shí)相關(guān)性最大,表示功放的輸入信號(hào),表示功放的輸出信號(hào)。
        為了減少較大的運(yùn)算量,文獻(xiàn)[4]在此基礎(chǔ)上提出改進(jìn)形式,僅用加減法就可實(shí)現(xiàn)環(huán)路的延遲估計(jì)。其表達(dá)式可以寫為:
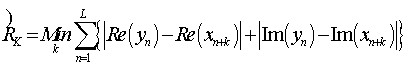        (2) 
        式中和分別表示信號(hào)的實(shí)部和虛部,表示輸入信號(hào)與反饋信號(hào)的時(shí)間差, 表示采樣數(shù)據(jù)長度。這種方法采用誤差疊加法,盡量放大兩信號(hào)差異,當(dāng)其值最小時(shí),可得其環(huán)路延遲的估計(jì)值。但其缺點(diǎn)是對(duì)信道畸變及高斯噪聲的抵抗力較差。
        為此,為解決信道畸變問題,文獻(xiàn)[8]提出幅度差值相關(guān)法:
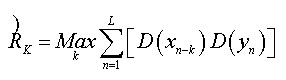        (3) 
        式中,幅度差定義為: 
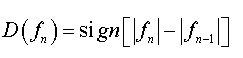       (4) 
       表示信號(hào)的幅度,且
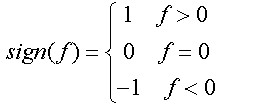       (5)
       該方法通過尋找到最大值從而得到延遲估計(jì)值,并且利用相鄰信號(hào)相關(guān)性,通過對(duì)相鄰信號(hào)取符號(hào)差運(yùn)算,提高了對(duì)信道畸變及高斯噪聲的抵抗力。但相較而言其運(yùn)算量引入了乘法運(yùn)算,并且在FPGA實(shí)現(xiàn)時(shí)需要復(fù)雜的時(shí)序控制,為此可以對(duì)其進(jìn)一步改進(jìn)。
        即在結(jié)合上述方法優(yōu)點(diǎn)的基礎(chǔ)上,令
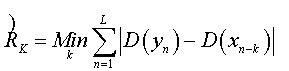       (6) 
        式中各量含義與前面表示相當(dāng),由表達(dá)式可知當(dāng)功放的輸入和輸出沒有延遲時(shí),數(shù)據(jù)差最小,即當(dāng)?shù)玫阶钚≈禃r(shí),就可以估測(cè)出環(huán)路延遲。重寫以上各式: 
        

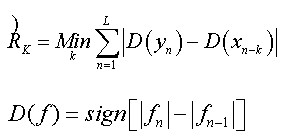
        式中
        
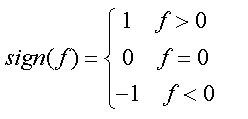
        這種方法因只需進(jìn)行加減法運(yùn)算,其運(yùn)算量較小,并且也可以有效提高對(duì)信道畸變及高斯噪聲的抵抗力,有利于FPGA的實(shí)現(xiàn)。

2.2、記憶多項(xiàng)式預(yù)失真器參數(shù)估計(jì)
        常規(guī)記憶多項(xiàng)式預(yù)失真器的參數(shù)估測(cè)方法中如式(10)中的列由下式生成:
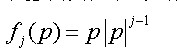        (7)
        但由于隨著列數(shù)增加會(huì)造成數(shù)學(xué)穩(wěn)定性問題,特別當(dāng)其不是正交矩陣時(shí)穩(wěn)定性問題更為突出[7]。因此,為了得到正交陣,可以利用以下函數(shù)生成矩陣的列向量,此時(shí)的幅度在0到1之間均勻分布:
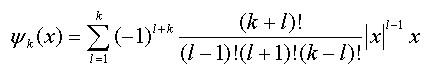        (8) 
        
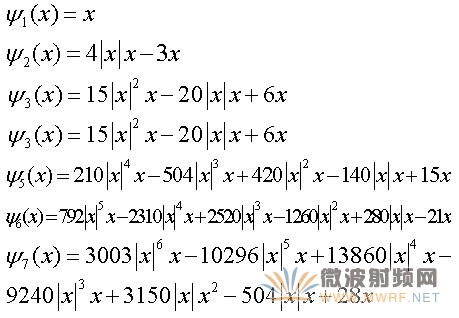
                                                                                                                (9)
        此時(shí),在常規(guī)多項(xiàng)式算法(式(7))中,功率放大器模型的輸出是以函數(shù)的加權(quán)和為基礎(chǔ)的,而在正交多項(xiàng)式算法(式(11))中,放大器模型的輸出則是以函數(shù)的加權(quán)和為基礎(chǔ)的。實(shí)際上,函數(shù)本身就是函數(shù)的加權(quán)和的估測(cè)。
        重寫常規(guī)多項(xiàng)式算法的表達(dá)式:
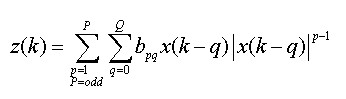        (10) 
        當(dāng)采用正交多項(xiàng)式算法時(shí),其表達(dá)式如下:
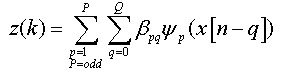        (11)
        式中即為估測(cè)參數(shù)。因此仍可以在最小時(shí)利用最小二乘算法估算出。

3、反饋回路的延遲估計(jì)實(shí)驗(yàn)驗(yàn)證
3.1、實(shí)驗(yàn)測(cè)量平臺(tái)

功率放大器輸出測(cè)試結(jié)果的可靠性和高精度性一直是研究的熱點(diǎn),本文采用的測(cè)試系統(tǒng)如圖2示。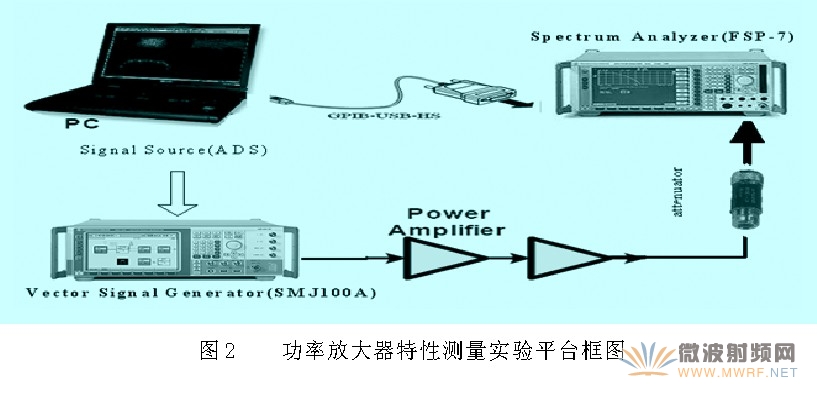

測(cè)量平臺(tái)的測(cè)試信號(hào)由ADS產(chǎn)生在PC中產(chǎn)生,然后通過通用接口總線(GPIB:General-Purpose Interface Bus)將PC中的信號(hào)下載到R&S的矢量信號(hào)發(fā)生器(SMJ100A)中。測(cè)量系統(tǒng)中的發(fā)射機(jī)功能是由矢量信號(hào)發(fā)生器和射頻功率放大器組成的。其中,矢量信號(hào)發(fā)生器完成基帶輸入信號(hào)的數(shù)模轉(zhuǎn)換并經(jīng)正交調(diào)制上變頻到所需頻段,被測(cè)對(duì)象選用Freescale( MHL21336)的AB類功率放大器。該測(cè)試系統(tǒng)的接收部分功能由R&S的頻譜分析儀(FSP—7)和PC共同構(gòu)成。頻譜分析儀將射頻信號(hào)下變頻、模數(shù)轉(zhuǎn)換及正交解調(diào),經(jīng)一系列處理后輸出的基帶I/Q兩路信號(hào)可以通過運(yùn)行PC中的MATLAB程序后由GPIB從頻譜儀中得到。

3.2、測(cè)量結(jié)果及分析

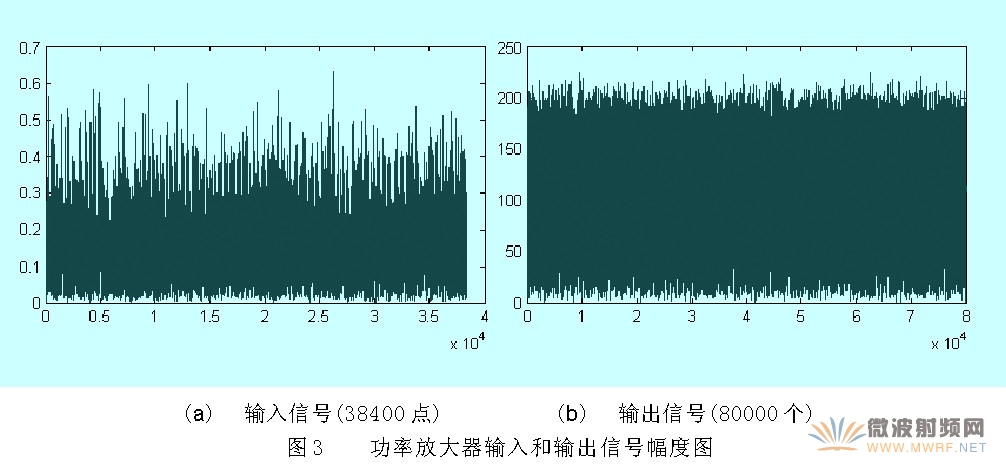
        當(dāng)輸入信號(hào)功率為-1dBm時(shí),輸入信號(hào)經(jīng)功率放大器、衰減器后采集到的輸出信號(hào)如圖3。

        圖3中橫坐標(biāo)表示采樣信號(hào)數(shù)據(jù)點(diǎn)數(shù),縱坐標(biāo)表示信號(hào)歸一化幅度,采用式(1-5)、式(1-6)、式(1-7)的方法,窗、次,從其中搜索得到最小值,其歸一化值如圖4所示。

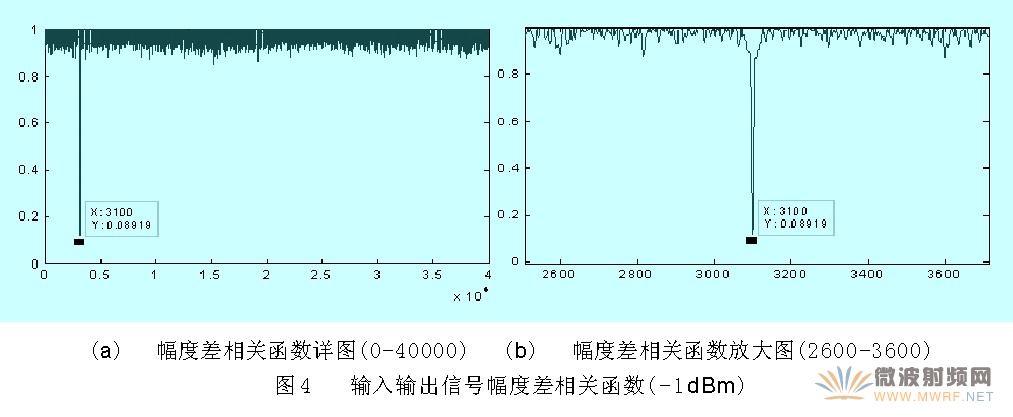
        可以看到在數(shù)據(jù)點(diǎn)為3100時(shí),幅度差相關(guān)函數(shù)取得最小值, 此時(shí)最大值歸一化為1,因?yàn)楣Ψ诺姆蔷€性特性及記憶效應(yīng)將導(dǎo)致輸出信號(hào)失真,將使輸入輸出相關(guān)性減小,故其幅度差相關(guān)函數(shù)不能減小到0,只是靠近0的一個(gè)較小的值,但這并不影響最終估測(cè)結(jié)果。

信號(hào)的環(huán)路信號(hào)最小幅度差相關(guān)函數(shù)也隨著輸入信號(hào)功率的變化而變化,其關(guān)系如表一所示。 

由表可以看出在輸入信號(hào)較小時(shí)最小幅度相關(guān)函數(shù)隨著功率增大變化不大,這是因?yàn)榇藭r(shí)信號(hào)在功率放大器的線性區(qū),相關(guān)性沒有因功率而嚴(yán)重惡化,但隨著功率增大輸入信號(hào)逐漸進(jìn)入非線性區(qū),相關(guān)性迅速惡化,最小幅度相關(guān)函數(shù)也迅速增大但并不影響最終估測(cè)結(jié)果。

4、反饋回路估計(jì)對(duì)預(yù)失真系統(tǒng)的影響比較

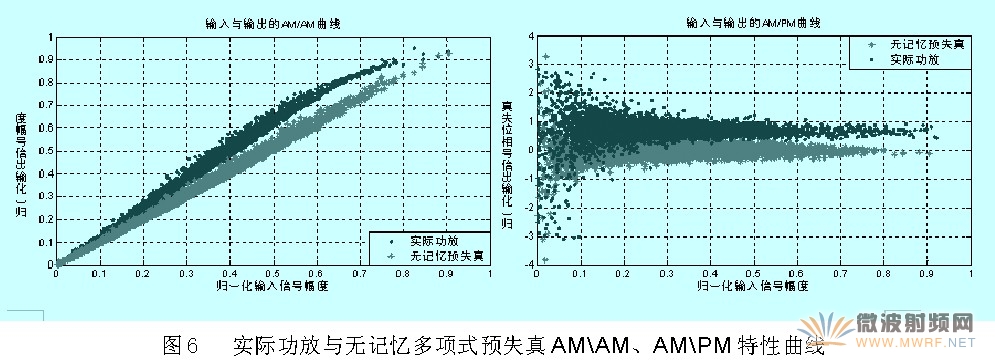
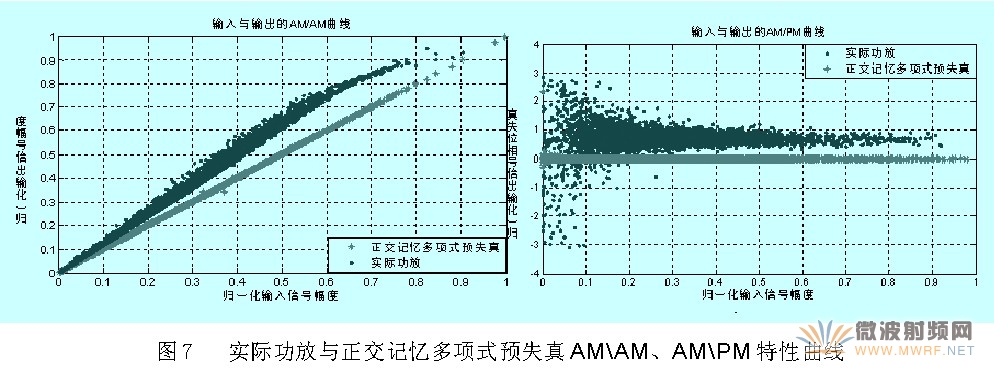
驗(yàn)證采用無記憶預(yù)失真和正交記憶多項(xiàng)式預(yù)失真方法比對(duì)反饋回路估計(jì)對(duì)系統(tǒng)的影響。采用正確反饋回路估計(jì)后可以得到功率放大器的AM\AM、AM\PM特性曲線,如圖6,7所示,可以發(fā)現(xiàn)在輸入WCDMA寬帶信號(hào)下,功率放大器表現(xiàn)出了明顯的記憶效應(yīng),其AM\AM和AM\PM特性已不再是一條一一對(duì)應(yīng)的曲線,而呈現(xiàn)出離散性。同時(shí),從AM\PM特性曲線可以看到,幅度較小的WCDMA信號(hào)更易受到歷史信號(hào)的干擾,因此較小信號(hào)的記憶效應(yīng)將更為嚴(yán)重,其特性也更為發(fā)散。

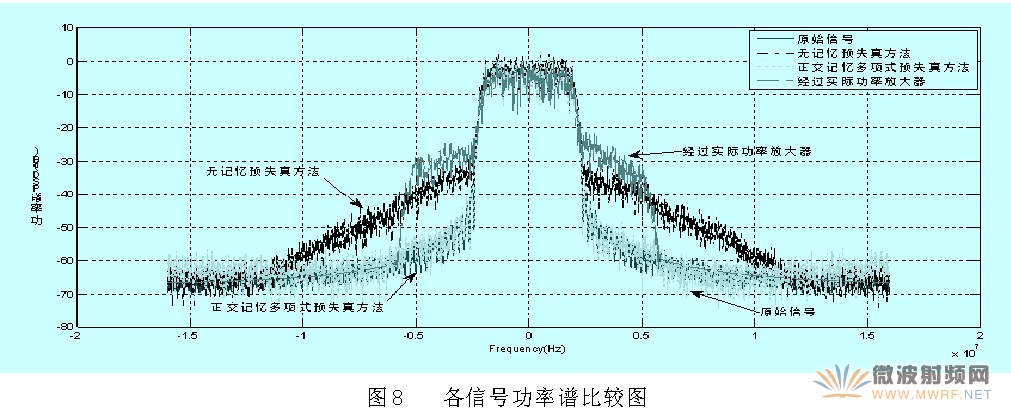
如圖8是各信號(hào)功率譜比較圖,從圖中可以看到在正確估計(jì)出反饋信息后無記憶多項(xiàng)式預(yù)失真器的單載波WCDMA信號(hào)的ACPR(鄰近信道功率比)改善近20dB,正交記憶多項(xiàng)式可以效果更佳,顯著地抑制鄰近信道的干擾,大約可以改善24 dB,從而證明了反饋回路估計(jì)算法的有效性。

5、結(jié)束語

本文首先給出了常規(guī)反饋回路估計(jì)算法,然后提出一種新的反饋回路算法,并采用一款射頻功率放大器驗(yàn)證其性能,結(jié)果證明了算法估算的可行性,最后采用無記憶預(yù)失真方法和正交記憶多項(xiàng)式預(yù)失真方法驗(yàn)證其系統(tǒng)性能,其鄰近信道功率比(ACPR)性能得到較大提高,證明算法的有效性。

參考文獻(xiàn):
[1] H.Holma,A.Toskala.WCDMA for UMTS. New York[M].John Wiley and Sons,2000:8-10.
[2] G.M.Calhoun.Third Generation Wireless Systems[J].Boston,MA:Artech House2003,1(1):10-16.
[3] 艾渤,楊知行,潘長勇等.高功率放大器線性化技術(shù)研究[J].微波學(xué)報(bào),2007,23(1):63-70.
[4] 艾渤,楊知行,潘長勇等.放大器預(yù)失真系統(tǒng)中的環(huán)路延遲估計(jì)[J].系統(tǒng)仿真學(xué)報(bào),2007,19(10):4487-4489.
[5] S.Wright,W.G.Durtler.Experimental performance of an adaptive digital linearized power amplifier[J].IEEE MTT-S,1992,41(4):395-400.
[6] Sala,H.Durney.Coarse time delay estimation for pre-correction of high power amplifiers in OFDM communications[C].In Proceedings of IEEE 56th VTC,2002,4:2313-2317.
[7] 趙洪新,陳憶元,洪偉.一種基帶預(yù)失真RF功放線性化技術(shù)的模型仿真與實(shí)驗(yàn)[J].通信學(xué)報(bào),2000,21(5):41-47.
[8] Hao Li,Dae Hyun Kwon,Deming Chen,et al.A fastdigital predistortion algorithm for radio-frequency power amplifier linearization with loop delay compensation[J].IEEE Journal of selected topics in signal processing,2009,3(3):374-383.