隨著行業的發展，功率和互調要求成為越來越多產品的瓶頸，因此，產品的功率和互調指標的好壞越來越成為衡量一個濾波器設計生產企業的技術水平的關鍵參數。本文主要針對在一定的單腔尺寸的前提下如何選擇諧振桿的最佳尺寸，使得其功率容量達到最佳狀態。

我們首先來分析一個單腔里面的電場分布及其強弱。眾所周知，一個諧振單腔內的電場主要分布在諧振桿上表面與蓋板、諧振桿內壁與調諧螺桿外表面之間，其他地方的電場很弱。在有功率通過該諧振單腔的時候，電場最強點是限制該單腔功率容量的關鍵點， 因此解決功率問題的關鍵就是想辦法降低電場最強點的電場強度。

現在我們就尋找一般情況下單腔里面的電場最強點在何處？假設單腔大小為a*b*c，諧振桿外半徑為Rout，內半徑為Rin，調諧螺桿半徑為Rsc，則調諧螺桿與諧振桿內壁之間的距離d1＝Rin-Rsc，諧振桿盤面與蓋板距離為d2。眾所周知，單腔在諧振情況下電場主要分布在兩塊區域：諧振桿盤面與蓋板之間、諧振桿內壁與調諧螺桿之間，必要時還需要考慮到諧振桿盤與側壁之間的電場（單腔較小頻率較低時） 。由于“木桶”效應，單純增加一個區域的功率容量（就是降低這個區域的電場強度）是不能起到增加單腔功率容量的目的的，要同時使兩個區域的電場強度都比較小，才能使單腔更不容易打火。

首先考慮諧振桿盤面與蓋板之間的電場， 如圖可以看見某個時刻諧振桿盤面與蓋板之間的電場分布。

由圖可見，1.當頻率較低（低于900M），諧振桿盤較大時，蓋板上的電場與盤面的電場幾乎一樣；

2.當頻率較高（高于1.8G），諧振桿盤面較小時，盤表面的電場會比蓋板面上的電場強，兩者的倍數關系與諧振桿盤面的大小有關。

再考慮諧振桿內壁與調諧螺桿之間的電場，下圖表示在某個時刻該區域的電場分布。

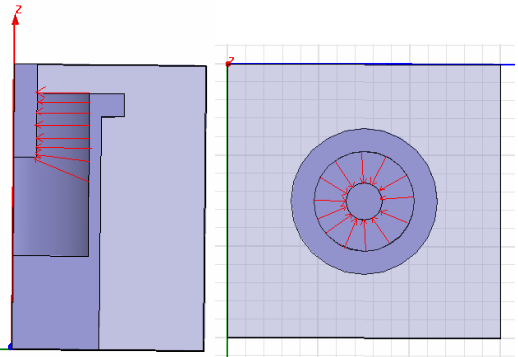
由圖可見，縱向上該區域電力線基本上是平均分布的，但在橫向上，電力線的分布明顯不均勻，越靠近調諧螺桿表面，電力線越密集，也就是電場越強。在調諧螺桿表面， 電場最強。 因為諧振桿內壁的電力線幾乎都中止在調諧螺桿表面，因此兩者的電場有如下關系：E 內壁（Ein）*S 內壁（Sin）＝E 螺桿（Esc）*S螺桿（Ssc），Esc/Ein＝Sin/Ssc＝2*pi*Rin/2*pi*Rsc＝Rin/Rsc。即兩者電場之比為兩半徑之比的倒數。

從上面的分析可以看出， 兩個區域電場最強的點分別在諧振桿上表面和調諧螺桿表面。 在此我們分析這兩者之間的關系， 當這兩個電場最強點的電場相等時，這兩塊區域就同時達到了最大的功率容量，因此該單腔就能達到最大的功率容量。假設某個時刻諧振桿與蓋板之間的電位差為V，則電場沿諧振桿盤面到蓋板面的線積分和沿著諧振桿內表面到螺桿表面的線積分相等，均為V。考慮兩種情況：

1. 頻率較低，諧振桿盤面較大時，諧振桿盤面到蓋板間的電場強度為恒定值Eup，則V＝Eup*d2＝（Esc+Ein）/2*d1，Eup*d2＝（Rsc/Rin*Esc+Esc）/2*d1＝Esc*（Rsc+Rin）/（2Rin）*d1兩區域最大電場相等，則，Eup＝Esc，d2＝（Rsc+Rin）/（2Rin）*d1上式即為該條件下要使單腔功率容量最大所需要滿足的等式。

舉個例子，諧振桿盤面距離蓋板3mm，調諧螺桿直徑為4mm，由上面的等式我們可以計算得到內徑的最佳值。

3＝（2+Rin）/（2Rin）*（Rin-2）

得到Rin＝6.6mm（約），即諧振桿內徑最佳值為13.2mm。

注：上面各等式均要求在滿足單腔諧振頻率的要求。

2. 頻率較高，諧振桿盤面較小，此時諧振桿盤面到蓋板間的電場強度不恒定，假設諧振桿盤面電場為Ecp，蓋板面電場為Etop，我們還是假設兩電場的平均電場強度為Eup，則Ecp>Eup，而Ecp＝Esc，則此時需滿足：

d2>（Rsc+Rin）/（2Rin）*d1

因此，在上面的例子中，如果諧振桿盤面很小，則諧振桿內徑最佳值應為Rin略小于6.6mm。

從上面的分析我們可以得出結論：

1.  頻率較低，諧振桿盤較大時，我們要盡量想辦法拉大諧振桿盤與蓋板間的距離，同時，要盡量滿足以下等式：d2＝（Rsc+Rin）/（2Rin）*d1，否則，調諧螺桿易打火。

2.  頻率較高時，我們要盡量把諧振桿的盤加大，盡量使諧振桿盤面上的電場均勻，同時滿足d2>(Rsc+Rin)/(2Rin)*d1。

3.  同時，我們也可以根據等式d2＝（Rsc+Rin）/（2Rin）*d1 分析在極限功率下使諧振桿盤先打火還是螺桿先打火。d2>(Rsc+Rin)/(2Rin)*d1,則為螺桿先打火，d2<(Rsc+Rin)/(2Rin)*d1,則為諧振桿盤面先打火。

4.  如果已經出現打火，改進功率時，不能一味的加大諧振桿與蓋板之間的距離，因為如果不改進諧振桿內徑尺寸，調諧螺桿一樣容易打火。