1.兩種濾波器都是數字濾波器。根據沖激響應的不同，將數字濾波器分為有限沖激響應（FIR）濾波器和無限沖激響應（IIR）濾波器。對于FIR濾波器，沖激響應在有限時間內衰減為零，其輸出僅取決于當前和過去的輸入信號值。對于IIR濾波器，沖激響應理論上應會無限持續，其輸出不僅取決于當前和過去的輸入信號值，也取決于過去的信號輸出值。

2.FIR：有限脈沖響應濾波器。有限說明其脈沖響應是有限的。與IIR相比，它具有線性相位、容易設計的優點。這也就說明，IIR濾波器具有相位不線性，不容易設計的缺點。而另一方面，IIR卻擁有FIR所不具有的缺點，那就是設計同樣參數的濾波器，FIR比IIR需要更多的參數。這也就說明，要增加DSP的計算量。DSP需要更多的計算時間，對DSP的實時性有影響。

以下都是低通濾波器的設計。

FIR的設計：

FIR濾波器的設計比較簡單，就是要設計一個數字濾波器去逼近一個理想的低通濾波器。通常這個理想的低通濾波器在頻域上是一個矩形窗。根據傅里葉變換我們可以知道，此函數在時域上是一個采樣函數。通常此函數的表達式為：

sa（n）＝sin（n∩）/n∏，但是這個采樣序列是無限的，計算機是無法對它進行計算的。故我們需要對此采樣函數進行截斷處理。也就是加一個窗函數。就是傳說中的加窗。也就是把這個時域采樣序列去乘一個窗函數，就把這個無限的時域采樣序列截成了有限個序列值。但是加窗后對此采樣序列的頻域也產生了影響：此時的頻域便不在是一個理想的矩形窗，而是成了一個有過渡帶，阻帶有波動的低通濾波器。通常根據所加的窗函數的不同，對采樣信號加窗后，在頻域所得的低通濾波器的阻帶衰減也不同。通常我們就是根據此阻帶衰減去選擇一個合適的窗函數。如矩形窗、漢寧窗、漢明窗、BLACKMAN窗、凱撒窗等。選擇一個具體的窗函數 之后，根據所設計濾波器的參數來計算所需的階數、此窗函數的表達式。然后用這個窗函數去和采樣序列相乘，就可以得到實際濾波器的脈沖響應。

IIR的設計（雙線性變換法）：

IIR的設計理念是這樣的：根據所要設計濾波器的參數去確定一個模擬濾波器的傳輸函數，然后再根據這個傳輸函數，通過雙線性變換、或脈沖響應不變法來進行數字濾波器的設計。它的設計比較復雜，復雜在于它的模擬濾波器傳輸函數H（s）的確定。這一點我們可以讓軟件來實現。然后，我們說一下它的具體實現步驟：首先你要先確定你需要一個什么樣的濾波器，巴特沃斯型，切比雪夫型，還是其它什么型的濾波器。當你選定一個型號后，你就可以根據設計參數和這個濾波器的計算公式來確定其階數、傳輸函數的表達式。通常這個過程中還存在預扭曲的問題（這只是雙線性變換法所需要注意的問題，脈沖響應不變法不存在這種問題）。確定H（S）后，就可以通過雙線性變換得到其數字域的差分方程。

3.對于IIR和FIR的比較，有些書上有論述。我引用陳懷琛的“數字信號處理教程－－MATLAB釋義與實現”：

從性能上來說，IIR濾波器傳遞函數包括零點和極點兩組可調因素，對極點的惟一限制是在單位圓內。因此可用較低的階數獲得高的選擇性，所用的存儲單元少，計算量小，效率高。但是這個高效率是以相位的非線性為代價的。選擇性越好，則相位非線性越嚴重。FIR濾波器傳遞函數的極點固定在原點，是不能動的，它只能靠改變零點位置來改變它的性能。所以要達到高的選擇性，必須用較高的階數；對于同樣的濾波器設計指標，FIR濾波器所要求的階數可能比IIR濾波器高5-10倍，結果，成本較高，信號延時也較大；如果按線性相位要求來說，則IIR濾波器就必須加全通網絡進行相位校正，同樣要大大增加濾波器的階數和復雜性。而FIR濾波器卻可以得到嚴格的線性相位。

從結構上看，IIR濾波器必須采用遞歸結構來配置極點，并保證極點位置在單位圓內。由于有限字長效應，運算過程中將對系數進行舍入處理，引起極點的偏移。這種情況有時會造成穩定性問題，甚至產生寄生振蕩。相反，FIR濾波器只要采用非遞歸結構，不論在理論上還是在實際的有限精度運算中都不存在穩定性問題，因此造成的頻率特性誤差也較小。此外FIR濾波器可以采用快速傅里葉變換算法，在相同階數的條件下，運算速度可以快得多。

另外，也應看到，IIR濾波器雖然設計簡單，但主要是用于設計具有分段常數特性的濾波器，如低通、高通、帶通及帶阻等，往往脫離不了模擬濾波器的格局。而FIR濾波器則要靈活得多，尤其是他易于適應某些特殊應用，如構成數字微分器或希爾波特變換器等，因而有更大的適應性和廣闊的應用領域。

從上面的簡單比較可以看到IIR與FIR濾波器各有所長，所以在實際應用時應該從多方面考慮來加以選擇。從使用要求上來看，在對相位要求不敏感的場合，如語言通信等，選用IIR較為合適，這樣可以充分發揮其經濟高效的特點；對于圖像信號處理，數據傳輸等以波形攜帶信息的系統，則對線性相位要求較高。如果有條件，采用FIR濾波器較好。當然，在實際應用中可能還要考慮更多方面的因素。

不論IIR和FIR，階數越高，信號延遲越大；同時在IIR濾波器中，階數越高，系數的精度要求越高，否則很容易造成有限字長的誤差使極點移到單位園外。因此在階數選擇上是綜合考慮的。

IIR濾波器（切比雪夫濾波）各濾波器比較（IIR和FIR，數字和模擬） 第19，20，21章內容，主要講IIR濾波器和濾波器的比較

IIR濾波不使用卷積運算，而是用遞歸(recursive)運算，因此執行速度很快，但在性能上不一定比FIR濾波好。IIR的沖擊響應由衰減性指數信號構成。

IIR輸入輸出的遞推關系式為：

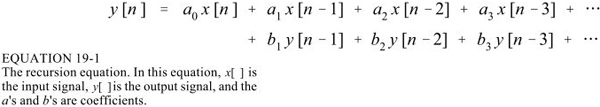
IIR遞歸系數和其頻率響應之間的關系可以通過Z變換來轉換，Z變換在此不涉及。

通過取不同的遞歸系數（下圖中的a和b），就可以實現不同的濾波：

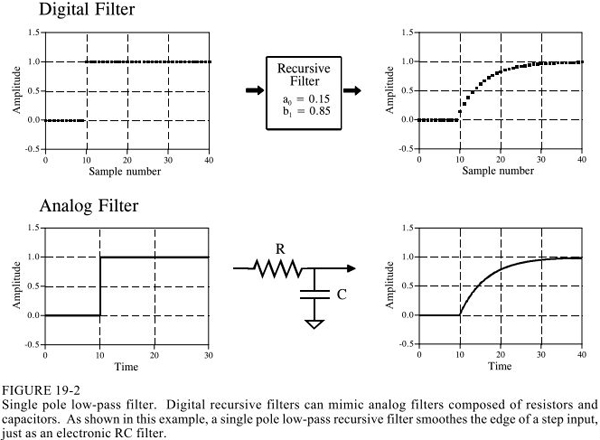
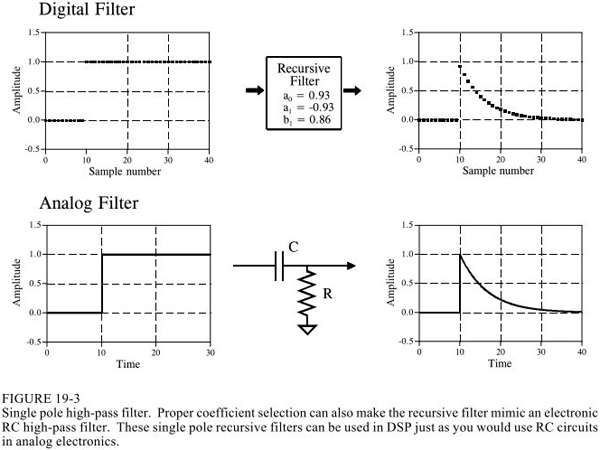
當然這是最簡單的應用，遞歸系數的取法有一定的講究和公式，這里略了。

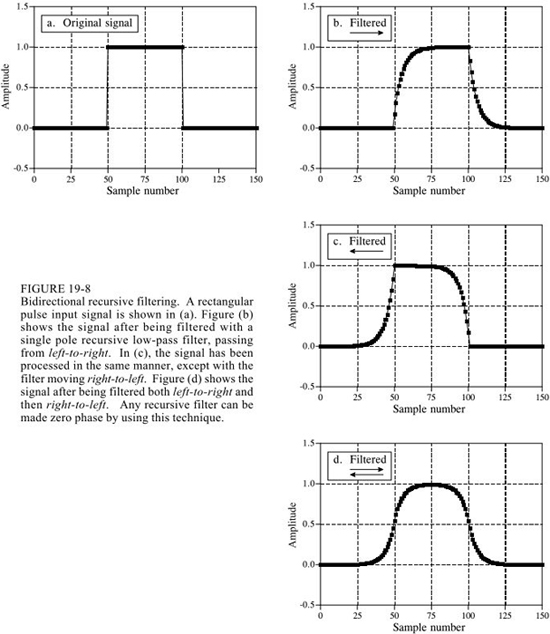
FIR可以做到是線性相位的，即沖擊響應是左右對稱的，而IIR通常是非線性相位的。這是因為FIR在設計的時候就確定了其時域波形和頻響，而IIR在設計中確定的是遞歸的系數，并不能決定其波形是什么樣子的。

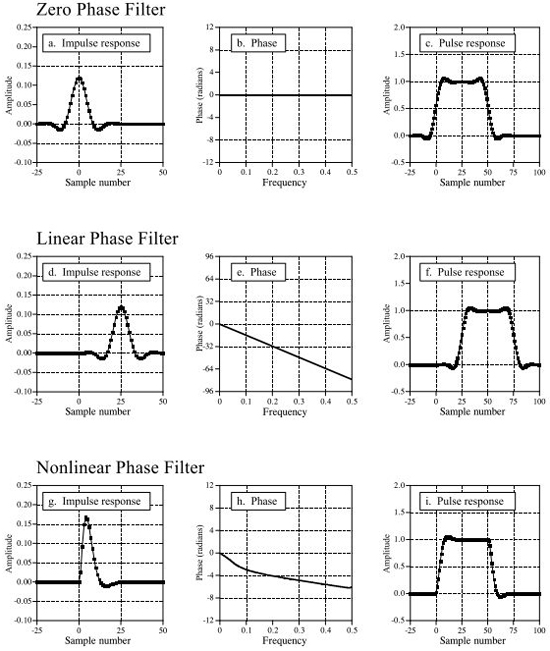
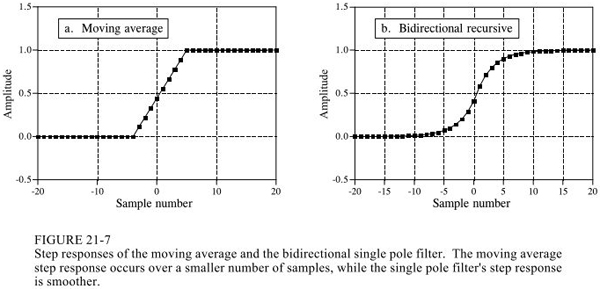
為了使IIR實現線性相位，可以進行雙向運算，如下圖所示：

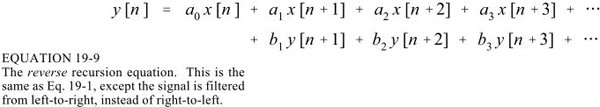
切比雪夫濾波

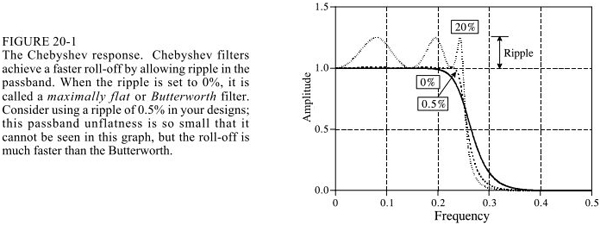
切比雪夫(Chebyshev)濾波是應用在頻域上分頻的，性能上當然不能和sinc窗函數濾波相比，但是它速度很快。

The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good).

對于極點的理解：

極點越多，性能越好。

通過查表可以確定濾波器的系數。

各種濾波器比較

1.模擬vs數字

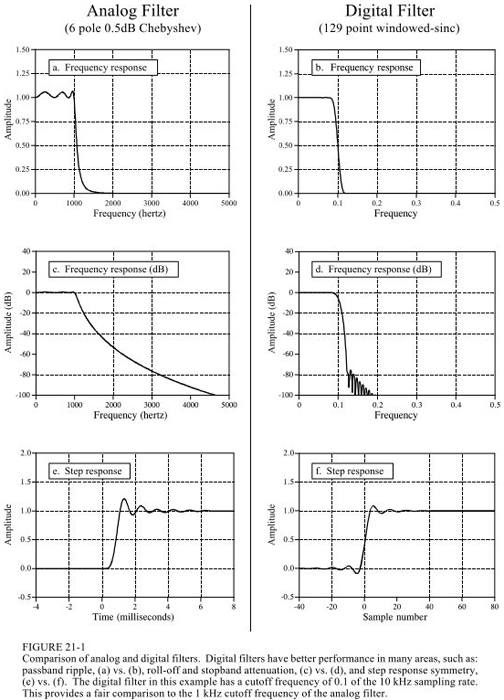
如果信號需要濾波，是在模擬階段濾波呢？還是數字化之后濾波？

下圖做了比較，可以看到數字濾波有著模擬濾波難以達到的性能，但是速度慢，而且模擬濾波的幅度以及頻率的動態范圍更大。

本例中模擬濾波的實現：

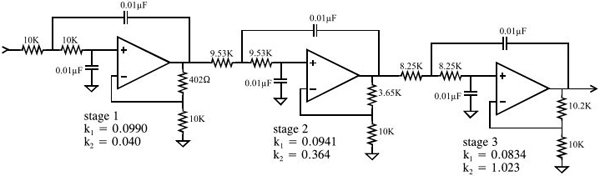
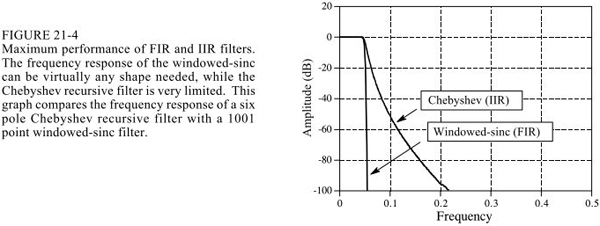
2.sinc窗函數vs切比雪夫

下圖做了比較

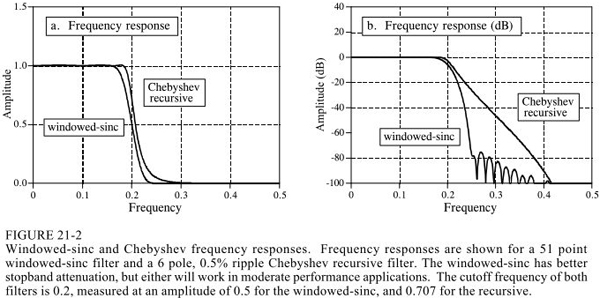
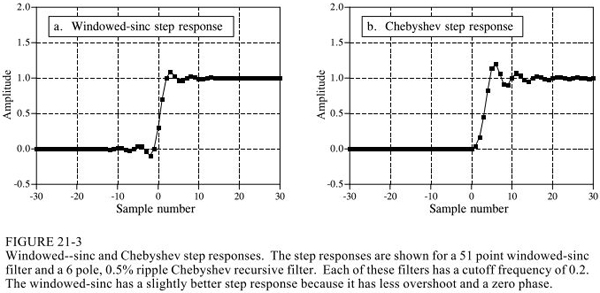
sinc窗函數是用卷積來運算，而切比雪夫是用遞歸方程。當然卷積可以用fft卷積來做，即先DFT然后頻域四則運算再DFT逆變換，這能提高速度，但是還是沒有遞歸方程快。另一方面sinc窗函數的濾波性能可以做的很好。

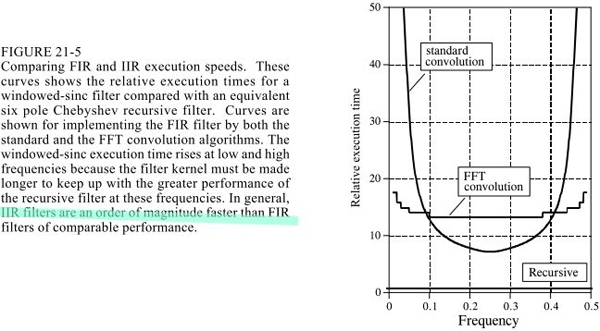
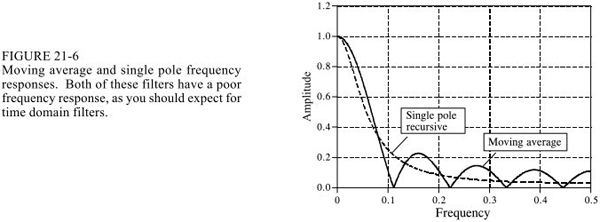
3.滑動平均vs單極點