圖中L為兩絕緣支撐之間的距離，l為絕緣支撐到基準面之間的距離L＝2l；B為絕緣支撐的厚度，L₁為絕緣支撐到外導體直徑變化處的距離。同軸腔中的諧振不僅由絕緣支撐內部的場決定，而且外部的空間距離也有相當大的影響，即兩個絕緣支撐之間的距離將影響諧振頻率，當L≥2D時，絕緣支撐之間的相互影響可減至較小，而當L＝3D時，絕緣支撐之間的相互影響完全可以忽略不計。絕緣支撐距外導體的直徑變化處L₁＝D時，相互影響減至最小，而當L₁＝1.5D時相互影響可以忽略不計。因此當L的取值小于D時，往往影響到射頻連接器的電壓駐波比。

2.4 過渡設計

在連接器的結構設計中，由于界面不同或配接的電纜的直徑不同，經常會遇到內、外導體直徑的變化，產生不連續(xù)電容。為了補償階梯產生的不連續(xù)電容，需要采取一定的補償方法，如果補償過渡設計不當，會嚴重影響射頻連接器的VSWR，對于過渡設計的結構，常用的結構如下：

2.4.1. 錯位過渡

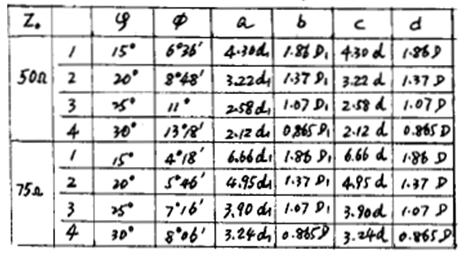
為了滿足導體直徑變化的需要，采用內、外導體錯開一段距離的辦法進行補償，也有人稱作階梯補償、直角補償?shù)取Ｈ鐖D5所示：粗端內、外導體直徑分別用d和D表示，細端內、外導體直徑分別用d₁和D₁表示，錯開的距離用a表示。

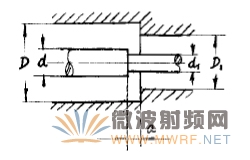
圖5.錯位補償示意圖

當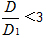＜3時，  
 
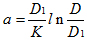
式中K是取決于特性阻抗的常數(shù)。
式中：當特性阻抗為50Ω時，K=3.09；
當特性阻抗為75Ω時，K=3.04。
當同軸線為固體介質同軸線時，

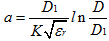
式中：K同上，ε_r為絕緣介質的相對介電常數(shù)。
當2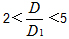＜＜5時，
空氣同軸線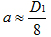 
固體介質同軸線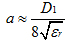

2.4.2. 錐體過渡

錐體過渡形式如圖6所示：

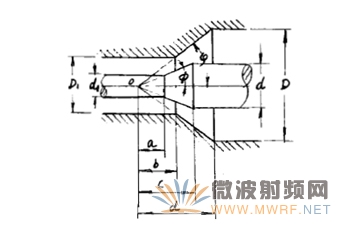
圖6.錐體過渡結構圖

錐體過渡又稱漸變過渡，這段過渡段的阻抗可按下式計算：

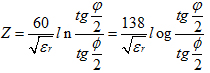
對于空氣介質段，則為：

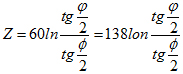
以上適用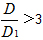時

2.4.3. 類中值過渡

在連接器直徑很小的情況下，在兩個特性阻抗截面之間可以進行補償
當Z₁＜Z_o和Z₂＞Z_o

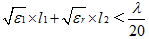
滿足：

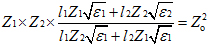
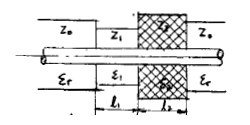
圖7.類中值過渡結構圖