1、引言

光子帶隙(photonic Bandgap-PBG)結構，又稱為光子晶體(photonic Crystal)，它是一種介質材料在另一種介質材料中周期分布所組成的周期結構。盡管光子帶隙最初應用于光學領域，然而由于其禁帶特性，近年來在微波和毫米波領域也獲得極大關注。在光子帶隙結構中,電磁波經周期性介質散射后,某些波段電磁波強度會因干涉而呈指數衰減,無法在該結構中傳播,于是在頻譜上形成帶隙。PBG結構的這種特性，在天線領域和微波電路中都有著巨大的應用價值。

時域有限差分(FDTD方法是分析PBG結構一種非常有效的數值計算方法。然而，由于微波光子晶體結構的精細，網格量必須很大，內存容量就成為計算中的瓶頸。此外當PBG結構為圓環形時，一般的階梯近似不足以滿足計算精度。針對以上兩個問題，本文采用本課題組帶有共形網格建模的MPI并行FDTD程序對圓環形PBG結構進行了分析。討論了單元數目，單元間距，圓孔內徑和導帶寬度對S參數的影響，最后設計了一種寬禁帶圓環形PBG結構。

2、圓環形光子帶隙微帶結構分析

FDTD作為一種時域方法，從最基本的Maxwell方程出發，具有廣泛的計算適用性，可以處理各種形狀和多種材料的復合結構系統，然而針對某些電大尺寸和精細結構，單機由于內存限制無法計算。最近，以PC機網絡集群系統為工作平臺的大型計算系統蓬勃發展，由臺式計算機構成這樣的系統無需任何額外的投資，也不會受到政策的限制，正因為如此，為并行計算提供了可行的、強有力的計算機硬件基礎。并行計算通過節點間的場值通信完成內存資源的擴展和計算時間的提高 (圖1)。MPI環境中并行算法的實現是國際上并行電磁計算研究的熱點和主流，所以本文的研究工作將基于MPI并行環境進行。此外，由于本文計算的是圓環形PBG結構，如果采用階梯近似來逼近光滑曲線,會導致嚴重誤差,還可能引起虛擬表面波,所以需要采用共形網格技術(圖2)，共形技術通過積分Maxwell方程修改FDTD原始迭代公式，可以準確處理變形網格。

二維微帶PBG除了中間一列外，其余位置電磁場值很弱，所以一維PBG和二維PBG結構的性能相差不大，而且一維結構結構緊湊，在實際當中有更大的優勢，所以本文重點分析的是一維PBG結構。設計的PBG微帶線周期結構采用圓環格子，單元間距為d，內徑為r，微帶線的帶寬為w，圓環寬度與導帶寬度w相同，如圖3所示。計算中邊界條件采用5層UPML吸收邊界，為了獲得頻帶特性，激勵源選擇高斯脈沖。將PBG結構的兩個端口插入UPML吸收邊界，并設置兩個參考位置，記錄參考面上的場值的時間變化，結合Fourier變換可以得到s11和s21參數。

3、數值仿真與試驗結果

計算模型如圖3所示的一維PBG微帶結構，微帶線基板等效介電常數為er=2.6，厚度為1mm。PBG結構兩端的帶線寬度為2.23mm，保證其特性阻抗為50Ω。微帶基板寬度為30mm。

A. 單元個數(units)變化

設d=6mm,r=2.75mm,w=0.5mm保持不變，分別計算了單元數(units)從3變到8的s21曲線，如圖4所示。

圖1 場值通信 圖2 共形網格

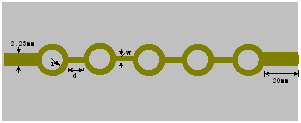
圖3 一維圓環形PBG結構示意圖

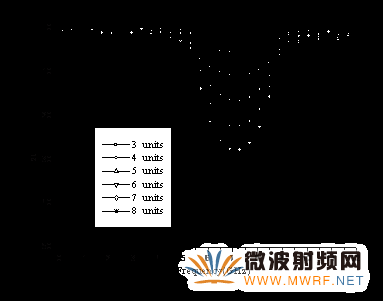
圖4 s21隨著單元數的變化

圖5 s21隨著單元間距的變化

從圖4中可以看出，禁帶的中心頻率不隨單元數而改變。隨著單元數(units)的增多，禁帶深度越大，禁帶寬度越窄，反之禁帶深度變小，禁帶寬度變寬。

B. 單元間距(d)變化

設r=2.75mm,w=0.5mm，單元數units=5，計算了單元間距d分別為3mm，6mm和9mm時的s21曲線，如圖5所示。從圖5中可以看出，禁帶的中心頻率隨著單元間距的改變而改變，單元間距變大，禁帶中心頻率向低端偏移，而且禁帶深度變大，反之向高端偏移，禁帶深度變小。禁帶寬度隨單元間距變化不大。

C. 圓孔內徑(r)變化

設d=6mm，w=0.5mm，單元數units=5，計算了圓孔內徑分別為2.25mm,2.75mm和3.0mm時的s21曲線，如圖6所示。從圖6中可以看出，禁帶的中心頻率不隨圓孔內徑的變化而變化。禁帶深度和禁帶寬度隨圓孔內徑而變化，半徑越大，禁帶深度越小，禁帶寬度越窄，反之，禁帶深度變大，禁帶寬度越寬。

D. 導帶寬度(w)變化

設d=6mm，單元數units=5，r=2.75mm ，計算了導帶寬度w=0.25mm，0.50mm和1.0mm時的s21曲線，如圖7所示。從圖7中可以看出，禁帶的中心頻率不隨導帶寬度的變化而變化。禁帶深度和禁帶寬度隨導帶變化而變化。導帶寬度越大，禁帶深度越小，禁帶寬度越窄，反之，禁帶深度變大，禁帶寬度越寬。

E. 寬禁帶PBG的實現

綜合考慮上述因素對禁帶性能的影響，我們設置w=0.25mm，r=2.25mm，d=9mm，units=8，圖8為計算得到的s21和s11曲線，可以看到在3.6GHz～8.5GHz范圍內形成一個非常明顯的寬禁帶。

圖6 s21隨著圓孔內徑的變化

圖7 s11隨著導帶寬度的變化

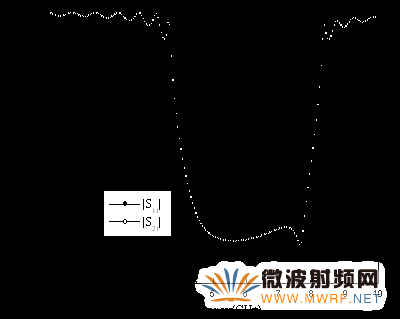
圖8 寬禁帶PBG的S參數曲線

4、結論

采用局部共形并行FDTD 技術分析了具有圓環形PBG結構的微帶濾波器,得到了其S參數. 從得到的結果可以看出,這種圓環形的PBG微帶傳輸結構具有明顯的禁帶特性,其禁帶中心頻率由單元間距決定,而圓孔的內徑，導帶寬度和單元數目影響著禁帶的寬度和深度. 通過調節這些可以參數可以獲得實際應用中所需要的禁帶特性.