0、引言

隨著多核技術(shù)的不斷發(fā)展，并行方法已經(jīng)成為一種處理較大規(guī)模問題的手段，同時(shí)在許多領(lǐng)域取得了成功地應(yīng)用。目前，并行算法的實(shí)現(xiàn)主要基于兩種標(biāo)準(zhǔn)：

MPI(Message Passing Interface)是一種基于消息傳遞并行編程模型的工業(yè)標(biāo)準(zhǔn)，主要用于分布存儲體系結(jié)構(gòu)的現(xiàn)實(shí)，是已被證實(shí)了的理想的程序設(shè)計(jì)模型;OpenMP標(biāo)準(zhǔn)，主要用于共享存儲體系結(jié)構(gòu)的并行編程，可實(shí)現(xiàn)在SMP 集群系統(tǒng)內(nèi)多處理器的多線程并行計(jì)算。

OpenMP是一個(gè)應(yīng)用程序接口，通過規(guī)范一系列的編程制導(dǎo)、運(yùn)行庫函數(shù)和環(huán)境變量來說明共享存儲體系結(jié)構(gòu)的并行機(jī)制，通常由于其較低的開銷和相對較簡單的編程而受到人們廣泛的關(guān)注。

時(shí)域有限差分(FDTD)方法是模擬計(jì)算電磁場的一種基本算法。自1966年Yee首次提出以來，經(jīng)過半個(gè)多世紀(jì)的發(fā)展，這一方法得到迅速發(fā)展和廣泛應(yīng)用。但是時(shí)域有限差分算法通常由于其串行方式使問題本身復(fù)雜化且運(yùn)算較費(fèi)時(shí)間而采用并行方式計(jì)算。因此，在PC機(jī)上研究并行FDTD算法問題，具有重要的理論與現(xiàn)實(shí)意義，可為大規(guī)模工程問題的并行化處理提供一定的方法借鑒與理論依據(jù)。本文以一維平面波在自由空間中的傳播為例，討論了采用OpenMP 技術(shù)對電磁場FDTD算法程序?qū)崿F(xiàn)并行化的方法，并將該并行方法在三維瞬態(tài)場電偶極子輻射FDTD程序中進(jìn)行了驗(yàn)證，也相當(dāng)于對該并行方法進(jìn)行了一定的推廣，并通過實(shí)驗(yàn)證明了該并行計(jì)算的有效性。

1、電磁場理論簡介

FDTD方法由微分形式的麥克斯韋(Maxwell)旋度方程出發(fā)進(jìn)行離散而得到的一組時(shí)域推進(jìn)公式。一維情況下，設(shè)TEM波沿z 軸方向傳播，介質(zhì)參數(shù)和場量均與x,y 無關(guān)，即- /-x = 0, -/ -y = 0 ,于是Maxwell方程為：

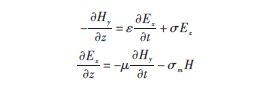
一維情況E 、H 分量空間節(jié)點(diǎn)取樣如圖1所示。

在自由空間中，σ = σm = 0 ,介質(zhì)為無耗，故而可得場的FDTD迭代方程為：

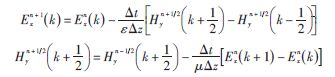
為了滿足數(shù)值計(jì)算的Courant穩(wěn)定性條件，通常選取時(shí)間步長為 Δt 空間間隔為 δ ,FDTD截?cái)噙吔鐥l件采用一階近似Mur,設(shè)截?cái)噙吔缣帪镋x 節(jié)點(diǎn)，如圖2所示，則在Ex 節(jié)點(diǎn)處離散，得：

式中： Ex (k - 1)為截?cái)噙吔鐑?nèi)的節(jié)點(diǎn);c 在真空中為光速c0,在介質(zhì)中則為截?cái)噙吔缣幉ǖ膫鞑ニ俣取?/p>

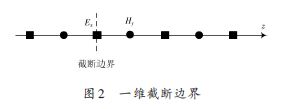
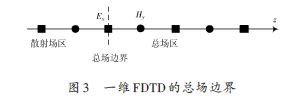
激勵(lì)源采用高斯脈沖源，其表達(dá)式為Ei (t)，其中τ 為常數(shù)，決定了高斯脈沖的寬度。為了使入射波限制在空間有限區(qū)域，根據(jù)等效原理，在區(qū)域分界面上設(shè)置等效面電磁流，并設(shè)分界面外的場為零。所以，在總場-散射場區(qū)的分界面上(總場邊界)設(shè)置入射波電磁場的切向分量便可將入射波只引入到總場區(qū)。本實(shí)驗(yàn)通過在一維FDTD 的總場邊界處引入高斯脈沖波，如圖3所示。

2、OpenMP 并行設(shè)計(jì)

2.1 OpenMP概述

OpenMP是基于共享存儲體系結(jié)構(gòu)的工業(yè)標(biāo)準(zhǔn)，它不是一門獨(dú)立的語言，而是對基本語言的擴(kuò)展，如C/C++,Fortran語言。其編程簡單，開銷小，規(guī)范并制定了一系列的編譯指導(dǎo)語句、運(yùn)行庫函數(shù)和環(huán)境變量。對于傳統(tǒng)的串行代碼，采用OpenMP技術(shù)并行化時(shí)無需對原程序作大的改動，只需加入一些簡單的編譯指導(dǎo)語句即可。同時(shí)，OpenMP 提供了兩種粒度的并行方式：粗粒度并行和細(xì)粒度并行。OpenMP的細(xì)粒度并行是指利用OpenMP 只求解循環(huán)部分計(jì)算，又稱為循環(huán)級并行。由此可見，細(xì)粒度并行是一種最為簡單的并行方法。

2.2 OpenMP并行編程模型

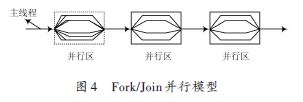
OpenMP采用標(biāo)準(zhǔn)的并行模式--Fork/Join式并行執(zhí)行模式，如圖4所示，在編譯過程中使用編譯指導(dǎo)語句實(shí)現(xiàn)并行化。在程序開始執(zhí)行時(shí)，只有主線程的運(yùn)行線程存在，在執(zhí)行的過程中，若遇到OpenMP 的指令要求并行執(zhí)行時(shí)，主線程會派生出子線程來執(zhí)行并行任務(wù)。在并行執(zhí)行的過程中，由主線程與派生出的子線程組成一個(gè)線程組來協(xié)同工作。在并行執(zhí)行結(jié)束后，派生出的子線程退出或掛起，不再工作，控制流程回到單獨(dú)的主線程中，直到下一個(gè)并行區(qū)或者程序執(zhí)行完畢。

2.3 FDTD算法的并行化

在用FDTD算法模擬計(jì)算電磁場的過程中，時(shí)間步長上的迭代過程是相關(guān)聯(lián)的、互相影響的，故而不能實(shí)現(xiàn)并行化。但是在一次迭代內(nèi)部，電場與磁場的計(jì)算僅需要前一時(shí)刻的計(jì)算結(jié)果，與其他區(qū)域的電場或者磁場分量無關(guān)，各個(gè)計(jì)算過程之間沒有影響、相互獨(dú)立，可以實(shí)現(xiàn)并行化。為此，本文采用OpenMP提供的細(xì)粒度并行的方式對該算法實(shí)現(xiàn)并行化，即OpenMP+細(xì)粒度并行。

3、并行FDTD 性能分析

3.1 仿真算例設(shè)計(jì)

為驗(yàn)證FDTD算法并行的性能，以電磁波在自由空間中傳播的一維FDTD 算法為例，采用OpenMP 提供的細(xì)粒度技術(shù)實(shí)現(xiàn)并行化。激勵(lì)源采用Gauss脈沖源，其帶寬為10 GHz,τ = 0.2 ns, t0 = 0.8 - τ = 0.16 ns,總場邊界為z0 = 500Δz 處，Δt = τ/ 80 = 0.002 5 ns, Δt = dz/ (2c)，吸收邊界采用一階近似Mur,波傳播的空間區(qū)域?yàn)楣?jié)點(diǎn)1~1 000.用統(tǒng)計(jì)的方法，分別測量了2 000~10 000 之間不同迭代次數(shù)的串并行時(shí)間。

3.2 并行性能測試

并行程序性能測試可由并行算法的加速比和并行效率來衡量，假設(shè)有n 個(gè)并行部件，則對加速比、效率的定義如下：

(1)加速比speedup=單一計(jì)算機(jī)運(yùn)行整個(gè)程序所花費(fèi)時(shí)間同一臺計(jì)算機(jī)使用n 個(gè)并行部件的執(zhí)行時(shí)間;

(2)效率efficiency= speedup n.

程序串并行的運(yùn)行時(shí)間由OpenMP 庫函數(shù)提供的OMP_get_wtime()函數(shù)來測量。具體地，在測量串行程序運(yùn)行時(shí)間時(shí)，注釋掉了程序中的并行編譯指導(dǎo)語句，并保持時(shí)間函數(shù)的位置不變。本文采用多次運(yùn)行程序取穩(wěn)定值的方法，分別測量并記錄了不同迭代次數(shù)下的程序串并行運(yùn)行時(shí)間。

3.3 測試環(huán)境

測試環(huán)境為Intel(R) Core(TM) 2 Duo CPUT5670@1.8 GHz,內(nèi)存為2 GB,操作系統(tǒng)為WinXP SP3,開發(fā)軟件為Intel Fortran 10.1.014 with vs 2005,測試結(jié)果如表1所示。

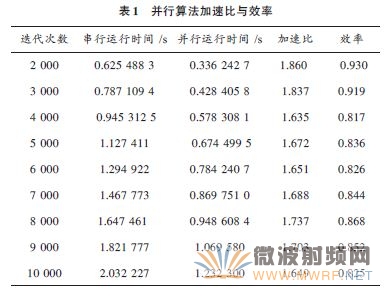
3.4 并行方法驗(yàn)證

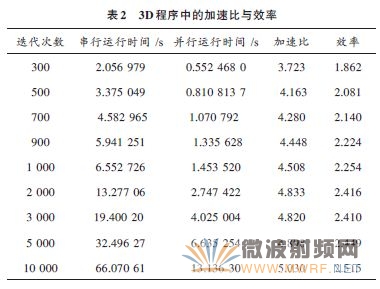
為了驗(yàn)證本文所采用的OpenMP 并行算法的可行性，將該并行方法應(yīng)用于三維瞬態(tài)場電偶極子輻射FDTD程序中。設(shè)整個(gè)計(jì)算域空間為真空，垂直點(diǎn)偶極子位于計(jì)算域中心，即Ez(0,0,0)，F(xiàn)DTD計(jì)算空間步長為5 cm,時(shí)間步長為83.333 ps,計(jì)算域?yàn)?5×55×55 個(gè)元胞，截?cái)噙吔鐬镸ur吸收邊界，輻射源為高斯脈沖，測量并記錄了300~10 000之間不同迭代次數(shù)的串并行時(shí)間，測量結(jié)果見表2.

4、結(jié)論

本文從分析OpenMP本身的特點(diǎn)及編程模型入手，結(jié)合一維FDTD算法實(shí)例，采用OpenMP+細(xì)粒度并行的方式實(shí)現(xiàn)了并行化，并證明了基于OpenMP 的并行FDTD 算法的有效性，而且并行FDTD 算法在所選測試實(shí)例的不同迭代次數(shù)上均獲得了超線性的加速比。充分利用了OpenMP共享存儲體系結(jié)構(gòu)的特點(diǎn)，避免了消息傳遞帶來的開銷，取得了較其他并行FDTD算法更快加速比和更高的效率。更值得一提的是，將該并行方法應(yīng)用在三維電磁場FDTD 程序中也取得了很好的加速比和效率，可以預(yù)見，該優(yōu)化方法在更復(fù)雜的算法中應(yīng)用一定具有更理想的性能提升。但不足之處在于系統(tǒng)的可擴(kuò)展性差，這是由于OpenMP 本身的特點(diǎn)所限制。

因此，今后的工作將放在對基于SMP 機(jī)群的MPI 與OpenMP混合編程模型的研究，從而克服系統(tǒng)擴(kuò)展性差的缺點(diǎn)，進(jìn)而提升系統(tǒng)的易用性和可移植性。