1、引言

機載相控陣天線方向圖的預測是電磁計算領域的一個帶有挑戰(zhàn)性的課題。由于機載平臺在很多工作頻段是電大尺寸的平臺，并且考慮到相控陣天線單元眾多，因此無法直接用商業(yè)軟件仿真模擬天線的受擾方向圖。而且，限于計算資源，單純采用有限元法(FEM)、矩量法(MOM)、時域有限差分法(FDTD)等數(shù)值計算方法難以實現(xiàn)。因此，比較務實的研究線路是以一致性幾何繞射理論(UTD)為主，計算機載平臺對天線方向圖畸變的影響。

本文結合實際工程，采用ANSOFT HFSS對天線單元進行仿真，然后按照天線陣列理論，采用方向圖乘積定理計算出天線陣列的未受擾方向圖。將此未受擾方向圖的矢量場分布取代天線陣列，作為“源”代入UTD算法，分析計算了載機對相控陣天線方向圖的影響，為機載天線位置優(yōu)化配置以及電磁兼容預測奠定了基礎。

2、計算模型和計算公式

UTD的繞射系數(shù)是通過平面波在理想導電劈上的繞射和在理想導電圓柱上的繞射兩個典型問題的解推廣得到的。在利用UTD分析機載天線輻射方向特性時，首先應將載機進行分解，分解成許多能利用UTD求解的典型部件的組合，如圖1所示。

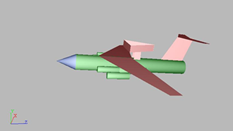
圖1 某飛機模型

模型由平板、圓柱和圓錐組合而成。由于UTD計算的目標要求是電大目標，因此一些細節(jié)部分做了適當?shù)暮喕？紤]到天線的安裝位置在飛機頂部，以及高頻算法的局部性原理，這樣的簡化在工程實踐中是可以接受的。因此，計算飛機體對天線輻射方向圖的影響就歸結為計算下列場分量：1)直射場;2)反射場;3)曲面繞射場;4)邊緣繞射場;5)二次及二次以上繞射場。其總散射場為各部分散射場之和：

(1)

其中，

為各類射線場(如直射、反射、繞射、高次繞射等)，

為飛機組件的總個數(shù)，

為該射線的遮擋因子(

=1，無遮擋;

=0，有遮擋)。

在利用UTD方法進行計算的時候，往往需要入射場。對于形式簡單的天線，比如單極子天線，反射點或者繞射點處入射場的求解是比較簡單的。然而對于相控陣天線這樣的復雜天線，要準確計算反射點或者繞射點處的入射場就變成一件非常困難的事情。為了解決這個問題，先對相控陣天線利用ANSOFT HFSS進行分析，得出天線的近區(qū)矢量場分量，以此作為起點，用UTD程序計算該近區(qū)場在通過機身的遮擋、反射、繞射以后的遠區(qū)效應。因此矢量場就成為UTD方法與HFSS的一個接口。

3、相控陣天線未受擾方向圖的估算

由于相控陣天線單元眾多，因此無法對整個天線陣列采用HFSS進行仿真。然而，天線陣列的未受擾近區(qū)矢量場分布又是下一步計算所必需的，因此只能采用方向圖乘積定理進行估算，將每一個單元的矢量場乘以陣因子，計算出整體天線陣列的矢量場分布。

本文研究的機載相控陣天線為80×8的平面陣列，天線工作頻率3.0GHz。天線單元如圖2所示，采用HFSS計算出的單元因子立體方向圖如圖3所示。

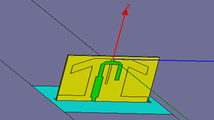
圖2 天線單元

圖3 天線單元方向圖

根據(jù)方向圖乘積定理，將單元因子與陣因子相乘得到陣列天線的立體方向圖，其中和波束方向圖如圖4所示，差波束方向圖如圖5所示。此時的方向圖都是未受擾方向圖，也就是飛機不存在時的立體方向圖。

(a)yoz面

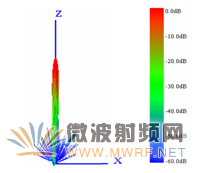
(b)xoz面

圖4 未受擾陣列天線和波束立體方向圖

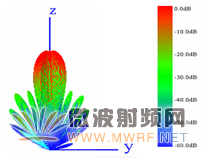
(a)yoz面

(b)xoz面

圖5 未受擾陣列天線差波束立體方向圖

4、計算結果

將HFSS計算得出的天線近區(qū)矢量場分量作為起點，用UTD程序計算該近區(qū)場在通過機身的遮擋、反射、繞射以后的遠區(qū)效應。

此時，只要尋出平板、圓柱和圓錐間的反射、繞射射線，就可以計算出天線經(jīng)過飛機機身的反射、繞射后的方向圖。然而，由于遮擋等其他因素，有些區(qū)域在經(jīng)過以上幾個模塊的計算以后仍然沒有場值，此時應該再加入像平板-圓柱、圓柱-平板以及圓柱-圓柱等二階的反射、繞射以及直射場。經(jīng)過這樣一些運算，就會得到經(jīng)過整架飛機的反射、繞射、遮擋以后的場值，最終得到天線安裝在飛機上時的受擾方向圖。立體方向圖如圖6所示。

(a) 和波束

(b) 差波束

圖6 受擾后陣列天線立體方向圖

圖7～9為二維方向圖，圖中直線是陣列天線未受擾的方向圖，點劃線是受擾后的方向圖。圖7是和波束俯仰面方向圖，相控陣天線位于飛機機身上方，由于機身的遮擋，在機身下方的場值明顯變小。而由于天線安裝位置，載機平臺對天線方位面方向圖的影響較小，如圖8所示。圖9是差波束方位面方向圖，零深達到了40dB，仍然能夠正常工作。

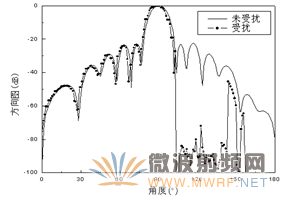
圖7 和波束俯仰面方向圖

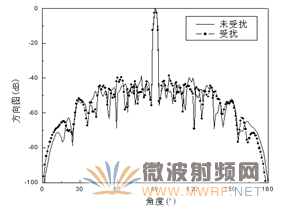
圖8 和波束方位面方向圖

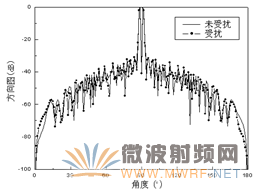
圖9 差波束方位面方向圖

5、結論

在分析像相控陣天線這樣比較復雜的天線的過程中，用ANSOFT HFSS軟件是比較方便的。然而由于有限元方法計算的局限性，ANSOFT HFSS又無法完全將機載天線與整架飛機在一起仿真計算其方向圖。對于計算飛機這樣的電大尺寸的問題，UTD方法概念清晰，簡單易算，是一種比較好的選擇，因此，可以將兩種方法結合使用，以計算機載相控陣天線的方向圖。從上面的例子可以看出，計算結果比較令人滿意，同時也證明了該方法的有效性，為工程應用提供了極有價值的參考依據(jù)。