鑒于國內外的很多ADS的資料都是微波射頻領域的，接下來，我們會慢慢的分享一些ADS在信號完整性領域經常使用的小功能和技巧。今天給大家介紹使用ADS進行串擾的仿真。

關于串擾的理論，大家可以參照《信號完整性分析》《信號完整性揭秘》等書籍。

大家都知道，串擾與很多因素有關系，如傳輸線耦合長度、信號的上升時間、傳輸線的間距等等。這里就以這三個因素舉例子對串擾做一些定性的分析：

在ADS中搭建仿真的拓撲結構，這一點非常的重要，因為要是拓撲結構搭建都有問題，那么就使得仿真結果變得不可分析，所以，在如下的仿真中，都盡量以單一變量做仿真實驗。

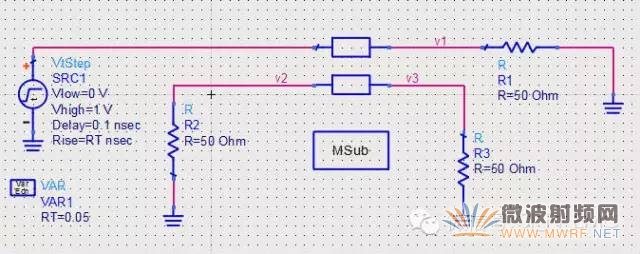
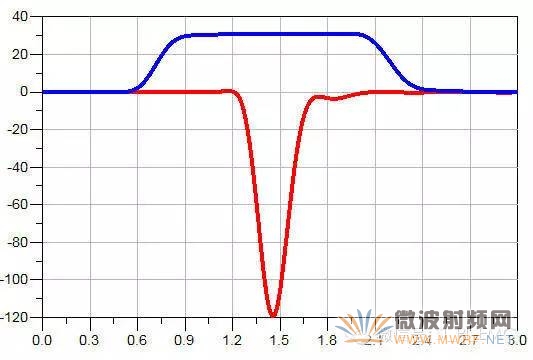
得到的串擾結果如下（藍色為近端串擾NEXT，粉色為遠端串擾FEXT）：

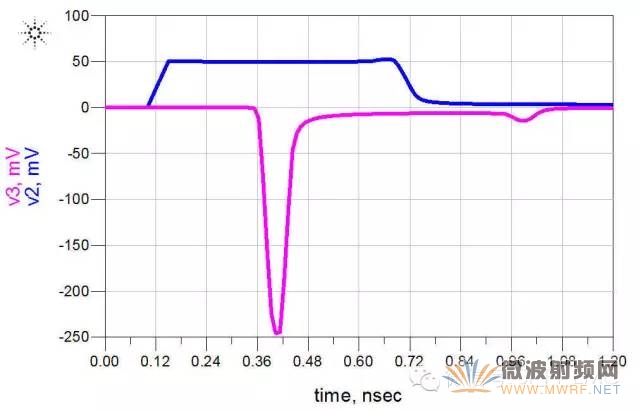
1、上升時間：考察上升時間時，其他的參數都不變，只改變上升時間的變量，所以需要加入變化參量和掃描參數，如下所示：

上升時間從50ps開始，300ns截止，每隔50ps仿真一次，得到的仿真結果如下：

顯然，隨著上升時間邊長，其遠端串擾變小，飽和長度變大。

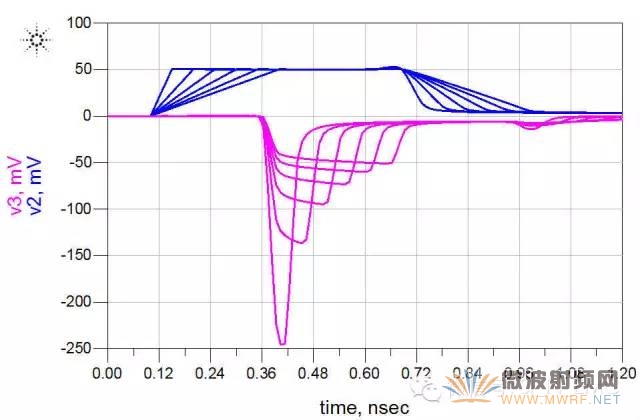
2、耦合長度：改變耦合長度，其他參數保持不變。長度由1inch開始，截止到6inch，每隔1inch仿真一次，變化參量和掃描參數如下：

得到的仿真結果如下：

隨著耦合長度的增加，其遠端串擾一直在增加，在1inch之前就已經達到飽和長度，所以在此實驗中，1inch之后增加耦合長度對近端沒有影響

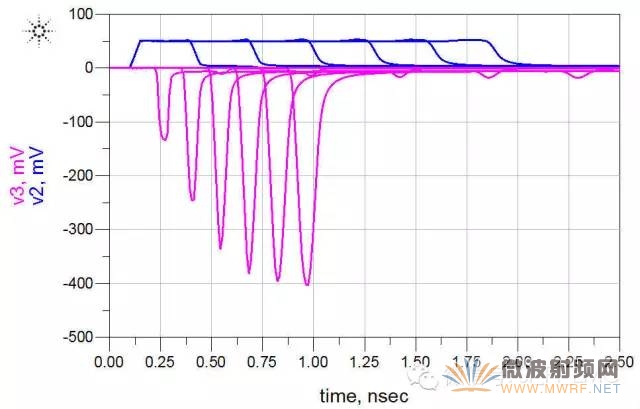
3、傳輸線間距：改變傳輸線間距，其他參數保持不變。間距由4mil開始，截止到10mil，每隔1mil仿真一次，變化參量和掃描參數如下：

得到的仿真結果如下：

由仿真結果可知，其間距越大，其近端串擾和遠端串擾都會變小。

由于ADS對數據的處理比較好，所以在以上實驗中，還可以進行很多數據的測量，這里只是講解串擾的參數sweep的仿真，所以沒有對數據處理做進一步的闡述，后面會專門做一篇數據處理的文章。

很多時候我們都在死記硬背很多公式和結論，記得住也記得對當然很好，但是如果記不住也不知道對不對，還不如使用一些仿真軟件對相關的問題進行仿真，這樣我們可以自己得到很多實用的經驗和結論。

歡迎關注：信號完整性（SI_PI_EMC）