I．介紹

在1952年，Schelkunoff和Friis[1]提出由于人工介質的磁導率持續增長，應該使用開環諧振器（SRR）。盡管他們提出了磁導率方程，但是在討論介電常數和磁導率的結果被否決后，他們沒有這么做。在1968年，Veselago[2]提出在不違反麥克斯韋方程和坡印廷定理的情況下，材料可能具有小于1甚至是負的介電常數和磁導率。看來，這個文件被忽視了近30年，直到Shelby，Smith和Schultz[3]通過制造一個有拆分環和細線結構的樣品，這個樣品在微波的頻率下的楔形容器內展示出了負折射，從而實驗式地驗證了Veselago的假說。Pendry和同事們[4]的開創性論文給了他們的實驗工作很多的援助[5]。在他們的第一篇論文中，Pendry等人描述了在有效媒介的介電常數低于等離子體頻率的情況下，周期性分布非常薄（小于0.01 λ）的電線是如何能引起類似血漿的行為，這取決于電線的寬度和間距以及介質嵌入的位置。在他們的第二篇論文中，他們描述了如何電動小分裂環的周期分布（約為0.1λ）可以產生一個有效的媒介，具有高度色散磁導率，在等效LC電路的共振頻率下可以成為負的。超材料的名稱被用來形容不尋常的這些材料的頻率響應，前綴“meta”在希臘字中，意思是“超越”[6]。在過去10年中，在超材料領域的研究已發生爆炸，數以百計的論文已經發表，其中大部分的理論提出超材料使用于各種微波和光學應用[7]–[12]。

我們用Schelkunoff和Friis使用過的方法，來獲得用RLC等效電路模型收集的小SRR的磁導率。如果入射磁場是垂直的SRR平面，感應電流的流經循環可以用下公式表示：
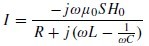（1）
其中ω為頻率，S是環路面積，Ho 為磁場的振幅，L是等效電感的SRR和C是電容的SRR的間隙，C是SRR間隙的電容。如果SRR是小電氣性的，則等效磁偶極矩的SRR可寫為Pm =IS。這類SRR集合的磁化強度（每單位體積的磁偶極矩）可以寫作：
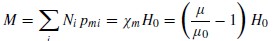（2）
其中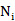 是第i個類型單位的SRR數量，Xm 是磁化率，μ是超材料的有效磁導率。通過帶入（1）中感應電流的表達式，我們可以寫出SRR的電感L、電容C和電阻R的有效磁導率。如下：
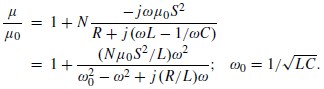（3）
我們觀察到，當該場的頻率與電路的共振頻率 =1/LC一致，我們可以得到一個大的磁導率值。因此磁超材料的透氣性，完全由于共振影響。遠離共振區域，超材料是無磁性的。等效電感L和電容C可以用不用的SRR幾何模型來算出。我們看到，這個簡單的推導，可以用感應電流的概念給出一個超材料的磁導率表達式，這與許多作者所用的Lorentz模型相同。通常被寫作
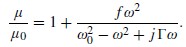（4）
我們把復介電常數和磁導率各自定義為ε' ±jε'' 和μ '''' '±jμ ''。物理學家更喜歡正號，而電氣工程師更喜歡負號。絕大多數的自然材料 ε ＞0，μ ＞0。金屬在光頻段ε  ＜0，μ ＜0。抗磁材料ε  ＞0，μ ＜1。所有的超材料在共振頻率，表現出高度分散行為。在共振頻率，傳輸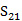（ ）始終是一個最小值，伴隨著在附近頻率下的反射最小值。根據共振的強度和性質，介電常數的實部、磁導率的實部，或者兩者一起，都能是負的。用Nicholson–Ross–Weir方法提取的介電常數和磁導率保證了材料是無源的，即復阻抗的實部是正的，波數的虛部導致了波在介質中的衰減。我們避免說明虛部是正的或是負的，由于虛部的正號或負號復屬性定義導致的可變性。當我們進一步得到介電常數的虛部和磁導率，超材料擁有的介電常數和磁導率有正值和負值。對于普通的介質材料，介電常數的虛部將滿足條件的因果關系。這對于負介電常數和負磁導率來實現負折射率是不是必須的。

微波異向介質的實驗表征，和平面超材料測量的S參數的提取出的復介電常數和磁導率是由Varadan和Tellakula完成的[13]。圖1顯示的SRR是一個電小差距的細線環。這種SRR結構可以導致電場和磁場的共振。當環軸與H場平行，SRR的H場產生電流，從而引起強大的磁偶極子，因此磁共振。如果SRR的間隙與E 場平行，E場在間隙中產生一個變化的電壓，導致了一個強大的磁偶極子，這會引起電諧振。對于一對對稱的SRR，磁共振受激，兩個SRR的磁偶極子應該加起來，而電偶極矩相互抵消[14]。對于電諧振，兩個電偶極子應該加起來，而磁偶極子抵消。

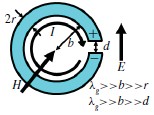
圖1 拆分環諧振器

在以前的實驗工作[3]，[13]-[19]，印刷電路板（PCB）技術和濕法刻蝕被用來沉積介質基片等金屬的共振結構例如FR4及Duroid。這些樣本可用于平面傳輸線樣品，其中波的傳播可以是在平面結構上或是垂直于平面結構。打個比方，這些在[3]和[13]中用的樣品，不能被用于實際應用。在本文中，對于3-D互連的超材料制造的低溫共燒陶瓷（LTCC），表現出的每種設計規范所表現出的超材料色散現象，我們提出了一種設計方法。LTCC工藝被廣泛用于工業微波和電子電路的封裝，多層電路技術，并用于方便嵌入無源器件，如電感，電容和電阻。它可以封裝提供的3-D電氣連接中間層，其中在所需的位置用金屬填充微通孔，這種能力也是很有吸引力的。LTCC工藝特別適合制作高頻系統啟動的封裝，用于天線陣列，單片微波集成電路（MMIC）等[21]-[24]。

LTCC工藝可以成功地用于3-D超材料的制造，并提供了很大的改善和很多的功能功能，相對于目前的用PCB平版印刷技術制造的2-D超材料方法。對于MMIC的應用，結合基板上無源但共振的超材料結構將有幾個優點。超材料的LTCC基板可以用來控制電磁干擾，并為內部的高頻元件和外部的干擾源提供隔離和條塊分割。

據我們所知，這是第一次系統地應用LTCC工藝來設計，制造和表征/驗證用于毫米波的超材料。在本文中，我們首先描述與LTCC制造步驟相匹配的3-D超材料制造的設計過程，以及將這個設計與2-D超材料相比較。然后，我們描述了這種使用Ansoft公司的高頻結構仿真（HFSS）的商業代碼的全波仿真的電磁建模結構。在數字化設計中，我們計算了一塊LTCC超材料板的S參數期望，和在燒制工藝中的收縮率期望。對于一些樣品，計算出的S參數被用來抽取超材料的介電常數和磁導率。這種設計后來使用自由空間測量系統而被制造和實驗特征化[13]。

圖2 杜邦951基板上的2-D SRR單元

將仿真和測量數據進行了比較，兩者符合得非常好。我們也提出了一種常用LTCC基板的復介電常數，杜邦951生瓷帶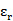（  =7.4−j0.026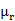， =1）的頻率范圍為5.8–110GHz。這個數據對于其他研究人員在其設計中使用杜邦951是非常有用的。

LTCC工藝對于超材料制作是一個非常容易和成本效益的方法。它是一個容易被封裝行業所接受的工藝，現在也在快速增長的超材料領域中有很好的應用。

II. LTCC超材料的設計過程

A．2-D超材料

首先，我們設計了LTCC介質基板的2-D SRR。單元如圖2。這種SRR是用銀墨印刷在一種杜邦951 LTCC薄膜上。它有用全波仿真器仿真的各種規模。基于有限元全波麥克斯韋求解，用Ansoft HFSS進行仿真。仿真一個周期陣列SRR的反射和透射系數，周期性邊界條件被用于單元的橫向邊界輻射邊界條件的取得，通過用一個完美的匹配層邊界條件來輸入和輸出平面波。

表I中，我們將在共振頻率下的每個SRR的半波長與SRR平均周長進行比較。共振頻率的頻率有一個最低的傳輸系數（S21 ）。半波長和平均周長按下面的方程計算：
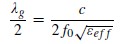（5）
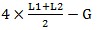平均周長= （6）
其中c=3×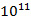 （mm/s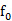）， 是SRR的共振頻率。由于SRR放置在空氣和LTCC基板之間，我們假設有效介電常數為4.2，這是空氣和杜邦951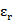（  =7.4）的平均介電常數。

表I共振頻率半波長及SRR結構的平均周長

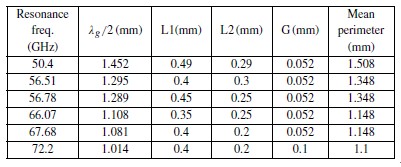
我們可以觀察到在各種情況下，平均周長要比半波長稍大一些。在共振頻率下，周長是半波長的整數倍時就會出現駐波。由于有效介電常數是近似值，所以有小的差異。空氣中50GHz下波長為6mm，基板厚度小于0.1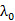 。薄基板能產生一個較低的有效介電常數。如果入射H場是垂直于2-D SRR軸，磁共振是不受激的[13]。

B．3-D超材料

3-D超材料是基于多層杜邦951 LTCC薄膜設計的，這可以使電諧振和磁共振都能發生。圖3為概念的示意圖。3-D SRR有一個由金屬線和兩個金屬填充的微通孔組成的環。金屬線是由金屬填充的微通孔立體連接的。微通孔的半徑為0.065毫米。允許收縮的相鄰SRR間距為0.87毫米。圖3展示了線寬尺寸、長度和間距。每條金屬線有一條與入射E場平行的間隙。3-D SRR的軸與H場平行。因此，3-D SRR 能被E場和H場受激。不斷仿真S參數直到我們得到了所需的共振頻率和別的特征，這種設計在幾次迭代后產生。

3-D SRR的平均周長為1.148mm（0.3mm×4-0.052mm）。因為SRR是完全嵌入在LTCC介質中的，用杜邦951（7.4）的電介質常數代替平均介電常數（4.2）來計算共振頻率，計算出來的共振頻率為48GHz。然而，SRR頂部和底部的金屬線受空氣影響，因此這個共振頻率只是一個簡單的粗略值，必須用全波仿真進行改善。預期的共振頻率是近50GHz，這是高于計算得出的共振頻率。我們需要有效地計算研究介電常數的研究。

III．3-D超材料的LTCC制造

設計好的3-D SRR是通過LTCC工藝制作的。首先應考慮綠膜的收縮。在共燒期間，綠膜收縮13%，因此SRR用于印刷的屏幕尺寸和通過填充的模板尺寸應該被放大。在烤箱中120 ℃下預處理30分鐘空白陶瓷綠膜后，用機械沖壓機打孔微通孔，并用杜邦6141銀漿填充中間層，如圖3（b）。在銀漿中用模具保護生瓷帶的其余部分。然后，用屏幕和杜邦6142D銀墨將金屬線印刷在底部上層和頂層的底部。在90 ℃的烘箱中干燥銀墨5分鐘后，每層在70 ℃和3500磅下層疊和層壓10分鐘。然后，LTCC在875 ℃下烘制15分鐘。圖4展示了共燒前層的照片。底層有SRR金屬線，中間層有金屬漿填充的通孔，金屬線印刷在通孔上。圖5中，制造的樣品被切開，和仿真的SRR進行比較。測量了幾個點的總厚度，樣品的厚度為0.284±0.003毫米。厚度收縮率略高于預期。我們還可以觀察到層對齊時，SRR的間隙移位。

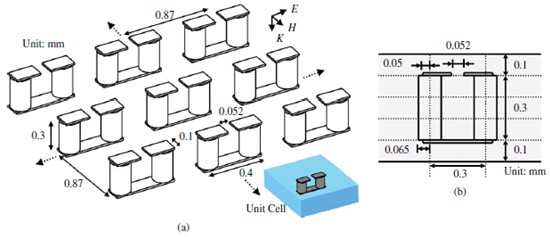
圖3 （a）杜邦951電介質的3-D SRR（b）側視圖

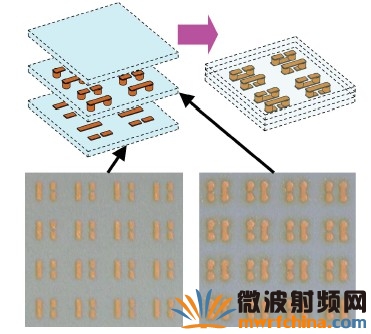
圖4 共燒前的每層照片。中間層有通孔和金屬線。底層只有金屬線。

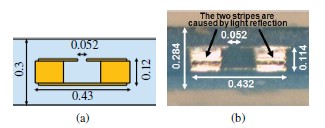
圖5 （a）仿真SRR的側視圖（b）共燒之后SRR制造的側視圖照片（單位：mm）

IV．用聚焦高斯光束的自由空間表征

LTCC 3-D SRR樣品是用自由空間測量系統測定的[13]，[25]。圖6展示的是一張照片和自由空間測量系統的示意圖。兩個有介質透鏡的喇叭天線是用于發送和接收集中的高斯光束平面波。LTCC超材料樣品被放置在兩個天線之間，通過完整的雙端口后，反映和線標定。向量網絡分析儀精確測量大小，杜邦951樣品（150mm×150mm）表面的反射相位和透射系數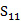（ 和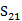 ），使用聚焦光束省去了原本需要的暗室。

使用尼科爾森羅斯威爾反演法[24]測量S參數，可以得到復介電常數和磁導率。圖7給出了一個用于頻率范圍為5.8–110 GHz的空白杜邦951 LTCC基板（厚度=1.047毫米）的介電常數。在65GHz以下我們用1.8毫米連接電纜，在67到110 GHz之間用1毫米的電纜。因此，65到67GHz之間的數據是缺失的。在整個頻率范圍內，杜邦951的介電常數（ ε ' ）的非常穩定的（7.4±0.2）。

圖8顯示了圖3中的3-D SRR樣品的仿真和實測數據。測量結果與仿真結果非常符合。測量的共振頻率（51.7GHz）比仿真略高（51 GHz），因為由于高于預期收縮，制作的幾何模型小于仿真的幾何模型。傳輸系數的測量幅度小于從48至53GHz的-10分貝。這是超材料的阻帶，如果在MMIC中，可以被用來作為一個過濾器或屏蔽材料。

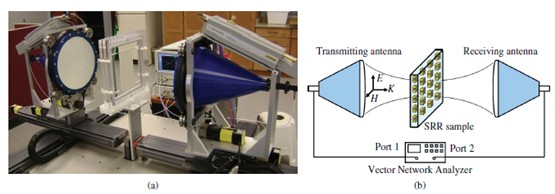
圖6 （a）照片（b）自由空間測量系統的示意圖

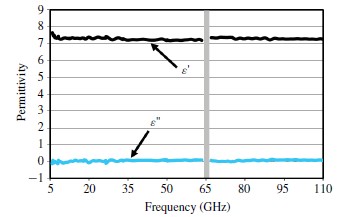
圖7 空白杜邦951基板的測量介電常數

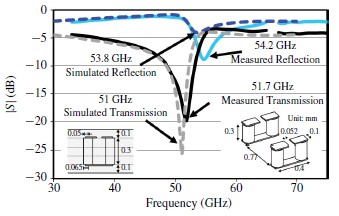
圖8 仿真和實測的杜邦951電介質的3-D SRR反射和透射系數

V．對稱雙3-D SRR

我們修改了用于雙共振的對稱雙SRR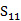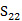（ = ）的單元，如圖9所示。相鄰對之間允許收縮的空間仍是0.87毫米。圖3顯示的3-D SRR有電諧振和磁共振，因為間隙平行于入射E場，軸平行于H場。然而，磁共振是如此之小，我們可以看到只有一個電諧振。磁共振可以由一個強大的對稱雙SRR之間的電容耦合增加。因此，我們也可以得到雙電磁共振[14]，[26]。

我們通過改變有通孔的中間層厚度，將兩種樣品，即三層和五層的樣本，認為是兩種樣品。圖9（b）和（c）為每個樣品的側視圖。由于增加了SRR的大小，五層樣品比三層樣品有更低的共振頻率。圖10顯示的是仿真反射的程度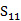（ ），B波段、V波段和W波段（33–110 GHz）的傳輸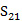（ ）系數。圖10（a）展示的五層樣品，我們觀察到| 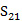|中45.2和56.6GHz下的兩個獨立的最小值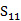，| |中43.8和60.8GHz下也有兩最小值。圖10（b）展示的三層樣品，|S21 |的最小值在74.4和94.2GHz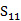，| |的最小值在73.6和102.8GHz。| |的最小值為SRR的共振。自從中間層厚度減少，SRR規模變小，三層樣品的共振頻率增加了30–40 GHz。

五層的樣本在45.2 GHz的共振，是一個磁共振，因為S11 的最小值（43.8 GHz）是之前S21 的最小值（45.2 GHz）。這解釋了之前[14]圖11（a）和（b）展示的45.2 GHz下的SRR表面電荷分布和電流方向。在相鄰SRR位置，H場激發了相同方向的電流和相反符號的電荷。因此，單元產生一個凈磁偶極矩，沒有凈電偶極矩，導致了磁共振。符號相反的SRR的電荷產生了一個耦合電容。在56.6 GHz的共振是電諧振，因為 的最小值（56.6 GHz）是之前 的最小值（60.8 GHz）。圖11（c）和（d）顯示了E場在間隙中產生了電壓變化，在相鄰SRR位置電荷密度有相同的符號。我們觀察到，有凈電偶極矩但無凈磁偶極矩，因為電流在相鄰SRR方向相反。

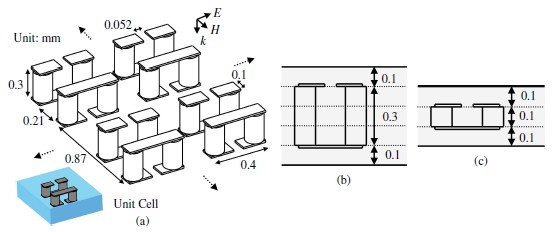
圖9 （a）LTCC電介質上對稱雙3-D SRR周期點陣（b）五層樣本的側視圖（c）三層樣本的側視圖

圖10 （a）五層樣品和（b）三層樣品的仿真反射系數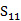（ ）和傳輸系數（ ）

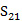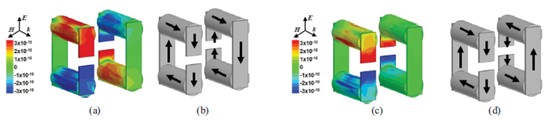
圖11 （a）45.2GHz的表面電荷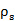（ ）（b）45.2GHz的表面電流分布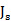（ ）（c）56.6GHz表面電荷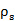（ ）（d）電流分布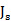（ ）（入射E場假定為1V/m）

VI．對稱雙3-D SRR的實驗表征

用自由空間測量系統的對稱樣本還有一個特點。圖12展示的是測得的空白的電介質和SRR介質的傳輸系數。65到67GHz之間的測量數據缺失，因為在這個波段不能使用1和1.88mm的電纜。圖10展示了45.2和56.6GHz下五層樣品耳朵仿真數據有雙共振。然而，在略高于46.6和60.2頻率下，測量數據有共振，這是由樣品的收縮比預期高造成的。圖5顯示的是歸因于對準誤差產生的一些錯誤。我們在屏幕印刷和堆積層中用對準標記。準誤差產生了超材料結構電長度的變化，自從結構被嵌入在陶瓷基板上，共燒后準誤差的影響很難評估。此外，LTCC工藝中微觀結構的收縮可能不平衡。頻移的響應很大，因為在毫米波段其波長很小。五層樣本中1.4GHz-3.6GHz的仿真數據和實測數據的共振頻率有差別。

當LTCC介電常數用于封裝，空白的介電常數沒有阻帶，波能通過整個波段的介質傳播。然而，在45-62GHz波段中，入射波不能通過SRR的LTCC介質傳播。圖3中SRR的阻帶增加了5到17GHz。對稱對屬性是由SRR的定位來改變的，即使規模和大小與圖3中的SRR相同。頻率范圍和通帶及阻帶的帶寬可以很容易地通過修改單元的結構設計。這對于允許理想信號進入包，防止不良信號滲入包的封裝有不錯的應用。

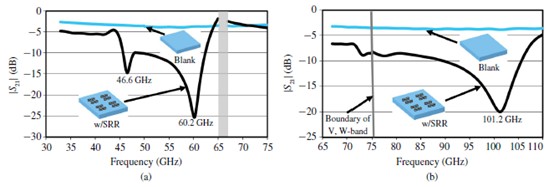
圖12空白電介質和SRR電介質的實測傳輸系數（ ）比較（a）五層樣品（b）三層樣品

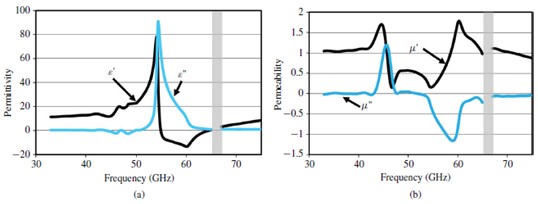
圖13 五層樣品實測數據計算出的有效（a）介電常數（b）磁導率

圖12（b）展示了三層樣本之間的比較。圖10（b）中74.4和94.2GHz的仿真數據有共振，101.2GHz的實測數據有共振。我們無法觀察到75GHz下實測數據的第一共振，因為它非常弱，而且接近V波段和W波段的臨界。仿真數據和實測數據的第二共振頻率差別在7GHz，這高于五層樣本。這表明對準誤差的影響可能與頻率成正比。在90–105GHz波段的SRR中，入射波無法通過三層LTCC介質傳播。

圖13提出的五層樣本的有效介電常數和磁導率是用尼科爾森羅斯威爾方法[13]，[25]測得傳輸和反射系數后計算得出的。介電常數和磁導率高度分散在共振頻率附近。因為電諧振，60.2GHz下介電常數的實部是負的。因為磁共振，46.6GHz下磁導率的實部接近于0。

VII．總結

我們已經證明，LTCC技術可以成功用于2-D和3-D形式的毫米波超材料制造。我們設計的超材料結構與LTCC工藝兼容，使用多層陶瓷膜進行設計。采用自由空間測量系統測量SRR的共振。測量結果與仿真數據相符合，除了對準誤差引起的頻率位移以及略高于期望收縮。這可以由更準確的對準方法和不同類型的超材料微觀結構收縮效應的系統化研究來改善。我們證明了材料的共振頻率可以通過改變SRR的大小來調整。通過簡單地引入一個LTCC材料的額外層，增加SRR三維高度的能力導致了成本的節約，因為不需要新的屏幕或者罩來實現其他的共振頻率。

我們設想將LTCC工藝用于許多不用的應用，包括如天線超材料、天線罩超材料、MMIC的無源基板元件，如過濾器、移相器、減少高頻EMI的封裝材料，如減少天線陣列的視覺和雷達信號的基板和覆蓋物。

感謝

我們非常感謝F.Barlow在開展低溫共燒陶瓷工藝時的指導和幫助，那時他是費耶特維爾的阿肯色大學教師。

作者：Vasundara V. Varadan，IEEE高級會員和In Kwang Kim，IEEE會員