算法的計算結(jié)果見圖3，圖3（a）中的尖峰是GSM所產(chǎn)生的隨機性射頻干擾，顯然，干擾的分布是隨機的，圖3（b）是中值濾波的結(jié)果，圖中這種隨機的RFI已經(jīng)被消除。

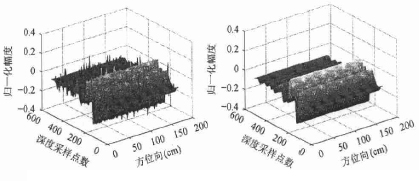
（a）中值濾波前的數(shù)據(jù)圖 （b）中值濾波后的數(shù)據(jù)圖

圖3、中值濾波前后的數(shù)據(jù)圖

4.2、算法的性能評估

4.2.1、干擾能量抑制比（IESR）

在抑制過程中，將RFI被對消的能量與SPR接收信號中RFI能量的比值，定義為IESR。它表示算法對RFI抑制的整體效果。由式（2）的模型，設(shè)接收信號為x（n）（n =0，…，N-1），s（n）為目標(biāo)回波信號，隨機噪聲為r（n）；抑制RFI后的輸出信號為y（n），殘余隨機噪聲為 r’（n），則干擾能量抑制比為

（9）

波形平均的干擾能量抑制比為IESR：97.496% 中值濾波的干擾能量抑制比IESR=99.672% 。圖4給出了波形平均算法的IESR與算法平均次數(shù)M的相對應(yīng)關(guān)系,可見隨M 的增大，IESR逐漸提高，但在M >10O時,IESR基本上保持不變，所以再增加波形平均的次數(shù)，算法的IESR沒有明顯提高。

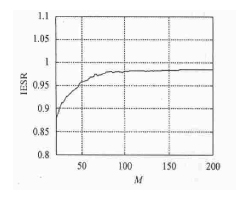
圖4、波形平均的IESR與平均次數(shù)M 的關(guān)系

4.2.2、且標(biāo)回波信號歸一化的均方誤差（NMSE）

IESR反映了隨機RFI抑制過程中，RFI被抑制的程度，但沒有考慮算法對SPR 目標(biāo)回波信號所造成的失真。現(xiàn)定義目標(biāo)回波信號的NMSE來量化RFI的抑制對目標(biāo)回波產(chǎn)生的影響，歸一化的均方誤差為

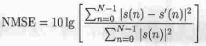（10）

式中s（n），s’（n）分別是RFI抑制前后目標(biāo)的回波信號，s（n）通常很難得到完整的解析式，所以式（10）是NMSE的理論計算式。在實際的計算過程，用屏蔽掉隨機RFI的接收回波，來作為s（n）代入計算。顯然，NMSE越小，RFI的抑制對目標(biāo)回波信號的影響越小，即信號的保真度越高。

4.2.3 、RFI抑制前后的SCR

RFI抑制之前的SCR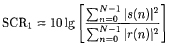₁
（11）

RFI抑制之后的SCR₂
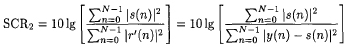（12）

綜合上述3項性能指標(biāo)，對波形平均算法、中值濾波算法和頻域陷波算法進行評定，見表1，其中處理增益△SCR=SCR₂-SCR₁，表明在RFI抑制的同時，算法對其它隨機噪聲抑制也有較好的效果。

表1、3種RFI抑制算法性能評估表

從表1中可以看出中值濾波算法的性能最優(yōu)良，它具有較高的RFI抑制能力，且能很好地保留目標(biāo)的回波信號，信號扭曲度最小，NMSE僅為-38.241dB；而且在RFI抑制的同時，能大幅度地提高目標(biāo)信號的信雜比，處理增益達到31.8414dB。波形平均算法的性能比中值濾波算法稍差一些；而頻域陷波算法的性能最差，對于隨機性的RFI，其性能遠(yuǎn)不及前兩種算法，基本上不能有效去除。

5、結(jié)束語

本文在時域用波形平均和中值濾波的方法，對UWB-SPR回波信號中由GSM 移動通信設(shè)備所產(chǎn)生的隨機射頻干擾進行了抑制，給出了波形平均和中值濾波的具體算法，用實測數(shù)據(jù)進行了驗證，結(jié)果表明波形平均和中值濾波都能有效快速地抑制隨機性的射頻干擾，其中中值濾波算法性能最優(yōu)良。

作者：李禹、粟毅、黃春琳、高守傳