現代通信中，IQ調制基本上屬于是標準配置，因為利用IQ調制可以做出所有的調制方式。

但是IQ調制到底是怎么工作的，為什么需要星座映射，成型濾波又是用來干嘛的。這個呢，講通信原理的時候倒是都會泛泛的提到一下，但由于這部分不好出題，所以通常不會作為重點。但換句話說即使目前國內的大部分講通信原理的老師，恐怕自己也就是從數學公式上理解了一下。真正的物理上的通信過程是怎么樣的，恐怕他們也不理解。所以說到底國內的通信課程，大多都停留在“黑板通信”的程度，稍微好一點的呢，做到的“仿真通信”的程度。離實際的通信工程差距很大。這一方面是由于通信系統確實比較龐大，做真實的實驗確實難以實施。另外一方面嘛，呵呵……

所以我決定還是要專門開貼來講一下這個問題，因為我理解這個問題大概用了兩年多的時間，到現在為止恐怕也不能算是完全搞明白了。每思至此，我總是會感慨通信博大精深，要做一名合格的通信工程師是非常不容易的。相反，想成為“專家”仿佛還要簡單一點，因為只需要抓住一點窮追猛打，至于其它的么……誰愿意研究誰研究，反正老子不管……

首先從IQ調制講起吧。所謂的IQ調制，冠冕堂皇的說法無法是什么正交信號如何如何……其實對于IQ調制可以從兩個方面來直觀的理解，一個是向量，一個是三角函數。首先說一說向量，對于通信的傳輸過程而言，其本質是完成了信息的傳遞。信息如何傳遞？信息本身是無法傳遞的，必須要以信號為載體，以物理世界中的信號某個特征來表示這個信息。那么有哪些特征可以表示呢，對于一個物理世界中存在的信號而已，無非就三個特征：相位、幅度、頻率。其中頻率和相位可以通過一定的關系等價出來。那么主要就是相位和幅度了。

好了，我們回到向量上面來。在一個二維平面里面，一個向量的信息同樣可以轉換為幅度（模）和相位（夾角）來表示。反過來時候，一個給定的向量，由于其模和夾角不同，可以通過該給定的向量表示一定的信息。如下圖所示的QPSK調制：

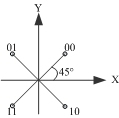
四個向量由于和X軸正半軸的夾角不同，可以分別表示出4個值。

再來看另外一個問題，如何生成這樣一個夾角不同的向量呢？這其實有時一個很簡單的數學問題：正交分解。任何一個向量都可以投影到X軸和Y軸上面做出兩個向量來。這樣我們就只需要改變X軸和Y軸上面的分量大小，就可以生成任意的向量。如X=1，y=-1時，就可以生成和X軸夾角315°模為根號2的這個向量。這條性質有什么用呢？后面我會解釋。

好了，到目前為止，這都是數學分析，所謂的正交分解，那首先是要找到兩個正交向量。在我們真實的物理世界里面去哪里找這兩個正交的向量呢。呵呵，還真有，而且是現成的。就是sin和cos。有性質cos（α+π/2）=sinα，二者正好相差九十度。至于這二者的正交性如何證明，我想這是數學老師的事情。反正現在已知有了這么兩個正交的東西了。有這兩個東西就太好了……為什么這么說呢，因為有了整個東西之后，抽象的正交分解就變成了高中都學過的三角函數了。

對于cos（wt+α）=cos（α）cos（wt）+sin（α）sin（wt），其中cos（α）和sin（α）都是常數，其實就變成了cos（wt）和sin（wt）的幅度了。換言之，改變cos（wt）和sin（wt）幅度，就可以得到任意的相位α。如果再狠一點，加一個系數Acos（wt+α）=Acos（α）cos（wt）+Asin（α）sin（wt），這其實還是改變的cos（wt）和sin（wt）幅度。就可以得到任意幅度、任意相位的cos函數，并可以利用這些函數去表示不同的信息。對此，通信原理上通常會用一種抽象的說法來約定表示方式，就是所謂的星座圖。

一個常見的16點QAM星座圖如下：

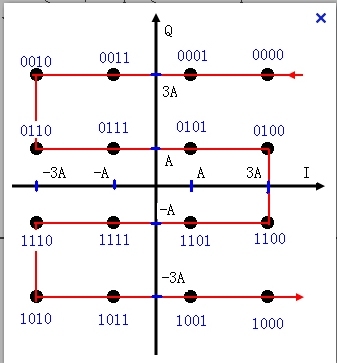
以I軸代表cos，而Q軸代表sin。從圖上可以看出，如果現在Acos（wt）+Asin（wt）可以求得一個向量（由于QQ空間沒有很好的數學編輯器支持，就不寫表達式了）。那么此時這個向量表示的是0101。而如果I軸上的值變為3A，換言之就是cos（wt）的幅度由A變為3A。就求得另外一個向量，該向量表示的是0100。 

在真實的電路中，我們是怎樣做到這一點的呢。這就和正交調制器有關了。下圖就是一個正交調制器的實例

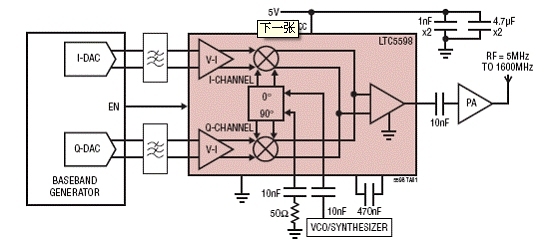
其核心是兩個乘法器。從VCO中出來的高頻余弦信號分別做0°和90°的相移，因此產生了cos（wt）和sin（wt），兩路正交信號。基帶信號通過I/Q兩路基帶信號進來，分別和cos（wt）和sin（wt）相乘，等效于調整了cos（wt）和sin（wt）的幅度值。最終等效成什么呢？就是控制I-DAC和Q-DAC的輸入從而產生不同幅度的電平信號。

所以，最終從基帶信號上面如何去控制產生已調信號，就變成了控制DA輸出的不同幅度值的信號。因此，要讓一個已調信號去表示某個信息，實際上就是把這個信息映射成I/Q兩個DAC輸出的幅度值。比如前面提到的那個星座圖，對于0100這樣一個數據實際上就是把它映射成I路的DAC輸出3A而Q路上的DAC輸出A。那么如何讓I-DAC輸出為3A而Q-DAC輸出為A，這就是和DAC的輸入輸出特性有關了。比如，這是一個雙極性4位的DAC，輸入為00時輸出為-3A，輸入為01時輸出為-A，輸入為10時輸出為A，輸入為11時輸出為3A。那么就如下圖所示

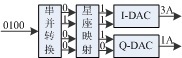
說到這里大家最終發現了，所謂的星座映射，其實就譯碼器而已……

但是上面那個圖，是不對的。原因是什么呢？就是這樣直接映射得到的都是方波信號。如果我們把中間的包括IQ調制解調、射頻收發的整個過程都等效成一個信道的話，那么可以抽象出這樣一個模型：

整個這個圖又讓我們回到了通信原理一開始就講的最基本的內容——基帶傳輸。對于基帶信號而言，通過信道以后會產生諸多畸變。其中最重要的畸變之一是由于通過一個帶限的信道，在頻域上可近似等價于和一個門信號相乘，而時域上則等價于和一個Sa信號卷積。如下圖所示左邊為時域Sa函數，右邊為等效低通的門信號：

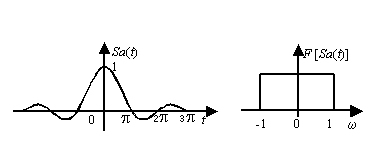
其結果就是本來應該是脈沖的信號在時域上產生了延拓，也就是拖尾……這樣相鄰的信號的幅度值就會和這個信號的拖尾疊加發生改變。改變的后果就是原本我們可能在發端映射的是I路3A，Q路A，但在收端卻變成了3A-x，和A+y。等效于引入了很大的噪聲。好在我們在通信原理中引入了乃奎斯特準則，給出了如果要無碼間串擾需要在發端加入成型濾波器，讓DA出來的值不是直挺挺的脈沖而是變成了某個形狀的波形。而這一過程是在星座映射之后，DA之前。

基帶成型濾波器基本流程如下

這樣DA出來的波形就是一個類似于余弦樣子的波形了。至于為什么這樣就沒有碼間串擾了，公式太多，QQ也寫不出來。

最后來說一下接收的問題。從上面的所謂發射的過程就是產生一個有特定幅度和相位的余弦信號的過程。而所謂的接收呢，其實本質就是反過來，是識別這個余弦信號的幅度和相位的過程。這個過程可以有很多辦法，我這里還是介紹最常見的IQ正交解調過程。

這個過程本質上來說還是一個三角函數的變換過程。上面說了，有三角函數：

Acos（wt+α）=Acos（α）cos（wt）+Asin（α）sin（wt)

如果要識別A和α，其本質其實上是識別Acos（α）和Asin（α）即可。

而這如何識別呢，考慮Acos（wt+α）*cos（wt）=Acos（α）cos（wt）*cos(wt)+Asin（α）sin（wt)*cos(wt)=1/2*Acos（α）(cos（2wt）+1)+1/2*Asin（α）sin(2wt)。對于這樣一個結果，我們很高興的發現，有一個常數項1*1/2*Acos（α）,而另外兩個屬于是高頻項。對于此，任何學過信號與系統的同學都應該明白，只需要用一個低通濾波器就可以把1/2*Acos（α）提取出來。1/2*Asin（α）的提取方法類似。

當然這只是理想的過程，實際中接收機遠比這個復雜，信號的識別過程也是有很多花樣的。