利用噪聲頻譜密度評(píng)估軟件定義系統(tǒng)中的ADC
不斷豐富的高速和極高速ADC以及數(shù)字處理產(chǎn)品正使過(guò)采樣成為寬帶和射頻系統(tǒng)的實(shí)用架構(gòu)方法。半導(dǎo)體技術(shù)進(jìn)步為提升速度以及降低成本做出了諸多貢獻(xiàn)(比如價(jià)格、功耗和電路板面積),讓系統(tǒng)設(shè)計(jì)人員得以探索轉(zhuǎn)換和處理信號(hào)的各種方法--無(wú)論使用具有平坦噪聲頻譜密度的寬帶轉(zhuǎn)換器,或是使用在目標(biāo)頻段內(nèi)具有高動(dòng)態(tài)范圍的帶限Σ-Δ型轉(zhuǎn)換器。這些技術(shù)改變了設(shè)計(jì)工程師對(duì)信號(hào)處理的認(rèn)識(shí),以及他們定義產(chǎn)品規(guī)格的方式。
噪聲頻譜密度(NSD)及其在目標(biāo)頻段內(nèi)的分布,能夠讓其在數(shù)據(jù)轉(zhuǎn)換過(guò)程中更好的被濾除。
比較在不同速度下工作的系統(tǒng),或者查看軟件定義系統(tǒng)如何處理不同帶寬的信號(hào)時(shí),噪聲頻譜密度(NSD)可以說(shuō)比信噪比(SNR)更為有用。它不能取代其他規(guī)格,但會(huì)是分析工具箱中的一個(gè)有用參數(shù)指標(biāo)。
我的目標(biāo)頻段內(nèi)有多少噪聲?
數(shù)據(jù)轉(zhuǎn)換器數(shù)據(jù)手冊(cè)上的SNR表示滿量程信號(hào)功率與其他所有頻率的總噪聲功率之比。
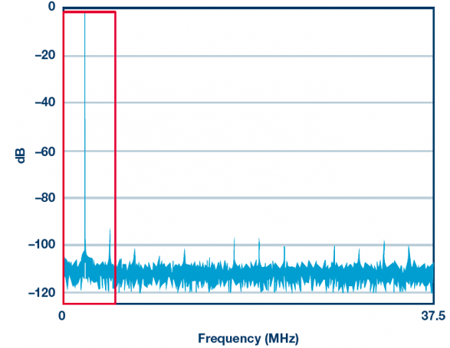
圖1. 9 dB調(diào)制增益的圖形表示:保留全部信號(hào),丟棄7⁄8噪聲。
現(xiàn)在考慮一個(gè)簡(jiǎn)單情況來(lái)比較SNR和NSD,如圖1所示。假設(shè)ADC時(shí)鐘頻率為75 MHz。對(duì)輸出數(shù)據(jù)運(yùn)行快速傅里葉變換(FFT),圖中顯示的頻譜為從直流到37.5 MHz。本例中,目標(biāo)信號(hào)是唯一的大信號(hào),且碰巧位于2 MHz附近。對(duì)于白噪聲(大部分情況下包含量化噪聲和熱噪聲)而言,噪聲均勻分布在轉(zhuǎn)換器的奈奎斯特頻段內(nèi),本例中為直流至37.5 MHz。
由于目標(biāo)信號(hào)在直流與4 MHz之間,故可相對(duì)簡(jiǎn)單地應(yīng)用數(shù)字后處理以濾除或拋棄一切高于4 MHz的頻率(僅保留紅框中的內(nèi)容)。這里將需要丟棄7⁄8噪聲,保留所有信號(hào)能量,從而有效SNR改善9 dB。換句話說(shuō),如果知道信號(hào)位于頻段的一半中,那么事實(shí)上可以在僅消除噪聲的同時(shí),丟棄另一半頻段。
這就引出了一條有用的經(jīng)驗(yàn)法則:存在白噪聲時(shí),調(diào)制增益可使過(guò)采樣信號(hào)的SNR額外改善3 dB/倍頻程。在圖1示例中,可將此技巧應(yīng)用到三個(gè)倍頻程中(系數(shù)為8),從而使SNR改善9 dB。
當(dāng)然,如果信號(hào)處于直流和4 MHz之間某處,那么就不需要使用快速75 MSPS ADC來(lái)捕捉信號(hào)。只需9 MSPS或10 MSPS便能滿足奈奎斯特采樣定理對(duì)帶寬的要求。事實(shí)上,可以對(duì)75 MSPS采樣數(shù)據(jù)進(jìn)行1/8抽取,產(chǎn)生9.375 MSPS有效數(shù)據(jù)速率,同時(shí)保留目標(biāo)頻段內(nèi)的噪底。
正確進(jìn)行抽取很重要。如果只是每8個(gè)樣本丟棄7個(gè),那么噪聲會(huì)折疊或混疊回到目標(biāo)頻段內(nèi),這樣將得不到任何SNR改善。必須先濾波再抽取,才能實(shí)現(xiàn)調(diào)制增益。
即便如此,雖然理想的濾波器會(huì)消除一切噪聲,實(shí)現(xiàn)理想3 dB/倍頻程的調(diào)制增益,但實(shí)際濾波器不具備此類特性。在實(shí)踐中,所需的濾波器阻帶抑制量與試圖實(shí)現(xiàn)多少調(diào)制增益成函數(shù)關(guān)系。另外應(yīng)注意,“3 dB/倍頻程”的經(jīng)驗(yàn)法則是基于白噪聲假設(shè)。這是一個(gè)合理的假設(shè),但并非適用于一切情況。
一個(gè)重要的例外情況是動(dòng)態(tài)范圍受非線性誤差或通帶中的其他雜散交調(diào)分量影響。在這些情況下,“濾波并丟棄”方法不一定能濾除雜散分量,可能需要更細(xì)致的頻率算法。
將SNR和采樣速率轉(zhuǎn)換為噪聲頻譜密度
當(dāng)頻譜中存在多個(gè)信號(hào)時(shí),比如FM頻段內(nèi)有許多電臺(tái),情況會(huì)變得愈加復(fù)雜。若要恢復(fù)任一信號(hào),更重要的不是數(shù)據(jù)轉(zhuǎn)換器的總噪聲,而是落入目標(biāo)頻段內(nèi)的轉(zhuǎn)換器噪聲量。這就需要通過(guò)數(shù)字濾波和后處理來(lái)消除所有帶外噪聲。
有多種方法可以減少落入紅框內(nèi)的噪聲量。其中一種是選擇具有更好SNR(噪聲更低)的ADC。或者也可以使用相同SNR的ADC并提供更快的時(shí)鐘(比如150 MHz),從而讓噪聲分布在更寬的帶寬內(nèi),使紅框內(nèi)的噪聲更少。
NSD進(jìn)入視野
這就提出了一個(gè)新問(wèn)題:如要快速比較轉(zhuǎn)換器濾除噪聲的性能,有沒(méi)有比SNR更好的規(guī)格?
此時(shí)就會(huì)用到噪聲頻譜密度(NSD)。用頻譜密度(通常以相對(duì)于每赫茲帶寬的滿量程的分貝數(shù)為單位,即dBFS/Hz)來(lái)刻畫噪聲,便可比較不同采樣速率的ADC,從而確定哪個(gè)器件在特定應(yīng)用中可能具有最低噪聲。
表1以一個(gè)70 dB SNR的數(shù)據(jù)轉(zhuǎn)換器為例,說(shuō)明隨著采樣速率從100 MHz提高到2 GHz,NSD有何改善。
表1.改變一個(gè)70 dB SNR的ADC的采樣速率
| Case 案例 |
Sample Rate 采樣速率 |
Nyquist BW 奈奎斯特帶寬 |
SNR | NSD | SNR in 50 MHz Band 50 MHz頻段SNR |
Oversampling Ratio for 50 MHz BW 50 MHz帶寬過(guò)采樣率 |
| A | 100 MSPS | 50 MHz | 70 dB | –147 dBFs/Hz | 70 dB | 1 |
| B | 500 MSPS | 250 MHz | 70 dB | –154 dBFs/Hz | 77 dB | 5 |
| C | 1 GSPS | 500 MHz | 70 dB | –157 dBFs/Hz | 80 dB | 10 |
| D | 2 GSPS | 1 GHz | 70 dB | –160 dBFs/Hz | 83 dB | 20 |
表2顯示了部分極為不同的轉(zhuǎn)換器的多種SNR和采樣速率組合,但所有組合都具有相同的NSD,因此每一種組合在1 MHz通道內(nèi)都將具有相同的總噪聲。注意,轉(zhuǎn)換器的實(shí)際分辨率可能遠(yuǎn)高于有效位數(shù),因?yàn)楹芏噢D(zhuǎn)換器希望具有額外的分辨率以確保量化噪聲對(duì)NSD的影響可忽略不計(jì)。
表2.幾種極為不同的轉(zhuǎn)換器均在1 MHz帶寬內(nèi)提供95 dB SNR;
SNR計(jì)算假定為白噪底
(無(wú)雜散影響)
| Sample Rate 采樣速率 |
Nyquist BW 奈奎斯特帶寬 |
Number of Bits 位數(shù) |
SNR | NSD | SNR in 1 MHz Band 1 MHz頻段SNR |
|
| Case 1 情形1 |
100 GSPS | 50 MHz | 8 | 48 dB | –155 dBFs/Hz | 95 dB |
| Case 2 情形2 |
10 GSPS | 5 MHz | 10 to 12 10至12 |
58 dB | –155 dBFs/Hz | 95 dB |
| Case 3 情形3 |
1 GSPS | 500 MHz | 14 | 68 dB | –155 dBFs/Hz | 95 dB |
| Case 4 情形4 |
100 MSPS | 50 MHz | 14 | 78 dB | –155 dBFs/Hz | 95 dB |
在一個(gè)傳統(tǒng)的單載波系統(tǒng)中,使用10 GSPS轉(zhuǎn)換器捕捉1 MHz信號(hào)似乎很滑稽,但在多載波軟件定義系統(tǒng)中,那可能是設(shè)計(jì)人員恰恰會(huì)做的事情。一個(gè)例子是有線機(jī)頂盒,其可能采用2.7 GSPS至3 GSPS全頻調(diào)諧器來(lái)捕捉包含數(shù)百電視頻道的有線信號(hào),每個(gè)頻道的帶寬為數(shù)MHz。對(duì)于數(shù)據(jù)轉(zhuǎn)換器而言,噪聲頻譜密度的單位通常為dBFS/Hz,即相對(duì)于每Hz滿量程的dB。這是一種相對(duì)量度,提供了對(duì)噪聲電平的某種“折合到輸出端”測(cè)量。還有采用dBm/Hz甚至dB mV/Hz為單位來(lái)提供更為絕對(duì)的量度,即對(duì)數(shù)據(jù)轉(zhuǎn)換器噪聲的“折合到輸入端”測(cè)量。
SNR、滿量程電壓、輸入阻抗和奈奎斯特帶寬也可用來(lái)計(jì)算ADC的有效噪聲系數(shù),但這涉及到相當(dāng)復(fù)雜的計(jì)算,參見(jiàn)ADI公司指南MT-006:“ADC噪聲系數(shù)--一個(gè)經(jīng)常被誤解的參數(shù)”。
過(guò)采樣替代方法
在較高的采樣速率下使用ADC通常意味著較高的功耗--無(wú)論是ADC自身抑或后續(xù)數(shù)字處理。表1顯示過(guò)采樣對(duì)NSD有好處,但問(wèn)題依然存在:“過(guò)采樣真的值得嗎?”
如表2所示,使用噪聲較低的轉(zhuǎn)換器也能實(shí)現(xiàn)更好的NSD。捕捉多載波的系統(tǒng)需要工作在較高采樣速率下,因此會(huì)對(duì)每個(gè)載波進(jìn)行過(guò)采樣。不過(guò),過(guò)采樣仍有很多優(yōu)勢(shì)。
簡(jiǎn)化抗混疊濾波--過(guò)采樣會(huì)將較高頻率的信號(hào)(和噪聲)混疊到轉(zhuǎn)換器的奈奎斯特頻段內(nèi).所以為了混疊影響,這些信號(hào)需要在AD轉(zhuǎn)換前被濾波器濾除。這意味著過(guò)濾器的過(guò)渡帶必須位于最高目標(biāo)捕捉頻率(FIN)和該頻率的混疊(FSAMPLE、FIN)之間。隨著FIN越來(lái)越接近FSAMPLE/2,此抗混疊濾波器的過(guò)渡帶變得非常窄,需要極高階的濾波器。2至4倍過(guò)采樣可大幅減少模擬域中的這個(gè)限制,并將負(fù)擔(dān)置于相對(duì)容易處理的數(shù)字域中。
即便使用完美的抗混疊濾波器,要最大程度減少轉(zhuǎn)換器失真產(chǎn)物折疊的影響也會(huì)帶來(lái)不足,在ADC中產(chǎn)生雜散和其他失真產(chǎn)物,包括某些極高階諧波。這些諧波還將在采樣頻率內(nèi)折疊,可能返回帶內(nèi),限制目標(biāo)頻段內(nèi)的SNR。在較高的采樣速率下,所需頻段成為奈奎斯特帶寬的一小部分,因而降低了折疊發(fā)生的概率。值得一提的是,過(guò)采樣還有助于可能發(fā)生帶內(nèi)折疊的其他系統(tǒng)雜散(比如器件時(shí)鐘源)的頻率規(guī)劃。
調(diào)制增益對(duì)任何白噪聲都有影響,包括熱噪聲和量化噪聲,以及來(lái)自某些類型時(shí)鐘抖動(dòng)的噪聲。
隨著速度更高的轉(zhuǎn)換器和數(shù)字處理產(chǎn)品的成熟,系統(tǒng)設(shè)計(jì)人員更頻繁地使用一定量的過(guò)采樣以發(fā)揮這些優(yōu)勢(shì),比如噪底和FFT。
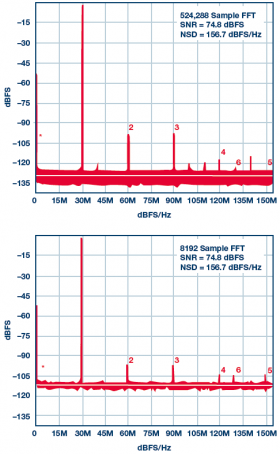
圖2. 524,288樣本FFT和8192樣本FFT的ADC
用戶可能很希望通過(guò)檢查頻譜曲線以及查看噪底深度來(lái)比較轉(zhuǎn)換器,如圖2所示。進(jìn)行此類比較時(shí),重要的是需記住頻譜曲線取決于快速傅里葉變換的大小。較大的FFT會(huì)將帶寬分成更多的頻率倉(cāng),每個(gè)頻率倉(cāng)內(nèi)累積的噪聲會(huì)變少。這種情況下,頻譜曲線會(huì)顯示較低的噪底,但這只是一個(gè)繪圖偽像。事實(shí)上,噪聲頻譜密度并未發(fā)生改變(這是改變頻譜分析儀分辨率帶寬的信號(hào)處理等效情況)。
最終,如果采樣速率等于FFT大小(或者成適當(dāng)比例),那么比較噪底是可以接受的,否則可能產(chǎn)生誤解。這里,NSD規(guī)格可用于直接比較。
當(dāng)噪底不平坦時(shí)
到目前為止,關(guān)于調(diào)制增益和過(guò)采樣的討論都假設(shè)噪聲在轉(zhuǎn)換器的奈奎斯特頻帶內(nèi)是平坦的。這在很多情況下是一個(gè)合理的近似,但也有某些情況不適用該假設(shè)。
例如,之前已經(jīng)提到調(diào)制增益并不適用于雜散,雖然過(guò)采樣系統(tǒng)在頻率規(guī)劃和雜散處理方面可能有一些優(yōu)勢(shì)。此外,1/f噪聲和部分類型的振蕩器相位噪聲具有頻譜整形性能,調(diào)制增益計(jì)算不適用于此類情況。
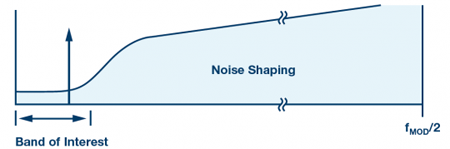
圖3.目標(biāo)頻段和噪聲整形
噪聲不平坦的一個(gè)重要情形是使用Σ-Δ型轉(zhuǎn)換器時(shí)。
Σ-Δ型調(diào)制器通過(guò)對(duì)反饋回路(量化器輸出)調(diào)制,進(jìn)而實(shí)現(xiàn)對(duì)量化噪聲整形,從而降低目標(biāo)頻段內(nèi)的噪聲,但代價(jià)是增加帶外噪聲,如圖3所示。
即使不進(jìn)行完整分析,也可以看到,對(duì)于Σ-Δ型調(diào)制器,使用NSD作為確定帶內(nèi)可用動(dòng)態(tài)范圍的規(guī)格尤為有效。圖4顯示的是高速帶通Σ-Δ型ADC放大后的噪底曲線。在75 MHz目標(biāo)頻段內(nèi)(中心頻率為225 MHz),噪聲為-160 dBFS/Hz左右,SNR超過(guò)74 dBFS。
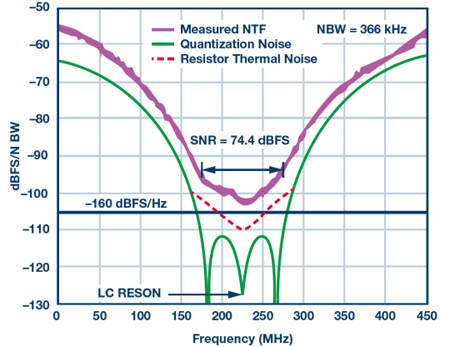
圖4.AD6676—噪底
一個(gè)總結(jié)性范例
為了總結(jié)并強(qiáng)化我們已經(jīng)討論過(guò)的內(nèi)容,現(xiàn)在看圖5所示曲線。本例考慮五款A(yù)DC:一款12位、2.5 GSPS ADC(紫色曲線);一款14位、1.25 GSPS ADC,時(shí)鐘速度分別為500 MSPS(紅色曲線);和1 GSPS(綠色曲線);一款14位、3 GSPS ADC,時(shí)鐘速度為3 GSPS(灰色曲線);一款不同的14位、500 MSPS ADC,時(shí)鐘速度為500 MSPS(藍(lán)色曲線);最后是圖4提到的帶通Σ-Δ型ADC。前五種情況的特征是具有近乎白色(平坦)的噪底,而Σ-Δ型ADC具有浴盆形噪聲頻譜密度,在目標(biāo)頻段內(nèi)的噪聲很低,如圖4所示。
在每種情況中,采樣速率保持固定,通過(guò)改變數(shù)字濾波器(其移除數(shù)字化處理后的帶外噪聲)的截止頻率來(lái)掃描信號(hào)帶寬。由此可得出幾點(diǎn)結(jié)論。
首先,降低信號(hào)帶寬會(huì)提高動(dòng)態(tài)范圍。然而,紫色、紅色和綠色直線的斜率始終為3 dB/倍頻程,因?yàn)槠銷SD曲線是平坦的。藍(lán)色曲線的斜率(Σ-Δ型ADC)則相當(dāng)陡峭。當(dāng)在通道的陡坡上掃描抽取濾波器的截止頻率時(shí),上述現(xiàn)象尤其明顯,因?yàn)樵擃l率的每次遞增/遞減都會(huì)導(dǎo)致濾除的噪聲功率量迅速變化。
其次,各曲線具有不同的垂直偏移,這取決于轉(zhuǎn)換器的NSD。例如,紅色和綠色曲線對(duì)應(yīng)相同的ADC。但綠色曲線(1 GSPS)高于紅色曲線(500 MSPS),因?yàn)槠銷SD比其他情況低3 dB/Hz,其時(shí)鐘是紅色曲線的兩倍。
圖5顯示了多種不同高速ADC的SNR與信號(hào)帶寬的權(quán)衡關(guān)系:五個(gè)斜率遵從平坦噪底的3 dB/倍頻程調(diào)制增益,而AD6676由于噪底整形而表現(xiàn)出更陡的調(diào)制增益。
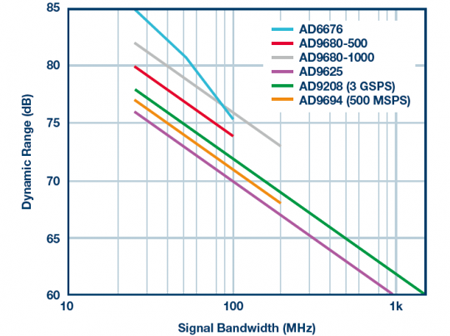
圖5.不同ADC的SNR與信號(hào)帶寬的關(guān)系
結(jié)語(yǔ)
不斷豐富的高速和極高速ADC以及數(shù)字處理產(chǎn)品正使過(guò)采樣成為寬帶和射頻系統(tǒng)的實(shí)用架構(gòu)方法。半導(dǎo)體技術(shù)進(jìn)步為提升速度以及降低成本做出了諸多貢獻(xiàn)(比如價(jià)格、功耗和電路板面積),讓系統(tǒng)設(shè)計(jì)人員得以探索轉(zhuǎn)換和處理信號(hào)的各種方法--無(wú)論使用具有平坦噪聲頻譜密度的寬帶轉(zhuǎn)換器,或是使用在目標(biāo)頻段內(nèi)具有高動(dòng)態(tài)范圍的帶限Σ-Δ型轉(zhuǎn)換器。這些技術(shù)改變了我們對(duì)信號(hào)處理的認(rèn)識(shí),以及我們定義產(chǎn)品規(guī)格的方式。
思考如何捕捉信號(hào)時(shí),工程師可能會(huì)想到去比較在不同速度下工作的系統(tǒng)。進(jìn)行這類比較,或者查看軟件定義系統(tǒng)如何處理不同帶寬的信號(hào)時(shí),噪聲頻譜密度可以說(shuō)比SNR更為有用。它不能取代其他規(guī)格,但會(huì)是規(guī)格列表上非常有用的一個(gè)目。
參考文獻(xiàn)
MT-006:“ADC噪聲系數(shù)--一個(gè)經(jīng)常被誤解的參數(shù)”。ADI公司,2014年。
作者簡(jiǎn)介
David H. Robertson自1985年從達(dá)特茅斯學(xué)院畢業(yè)后,便一直在ADI公司數(shù)據(jù)轉(zhuǎn)換器部門工作。他從事過(guò)采用互補(bǔ)雙極性、BiCMOS和CMOS工藝的各類高速DAC和ADC設(shè)計(jì)。他與美國(guó)、愛(ài)爾蘭、韓國(guó)、日本和中國(guó)的產(chǎn)品開(kāi)發(fā)團(tuán)隊(duì)合作,歷任產(chǎn)品工程師、設(shè)計(jì)工程師、產(chǎn)品線總監(jiān)和模擬技術(shù)副總裁。David目前是ADI公司高速轉(zhuǎn)換器部門的產(chǎn)品與技術(shù)總監(jiān)。
David擁有15項(xiàng)轉(zhuǎn)換器和混合信號(hào)電路方面的專利,參加過(guò)兩次“最佳小組”國(guó)際固態(tài)電路會(huì)議晚間小組談話,是榮獲《IEEE固態(tài)電路雜志》1997最佳論文獎(jiǎng)的論文的合著者。他從2000年至2008年擔(dān)任ISSCC技術(shù)計(jì)劃委員會(huì)委員,并在2002年至2008年期間擔(dān)任模擬與數(shù)據(jù)轉(zhuǎn)換器小組委員會(huì)主席。
Gabriele Manganaro擁有意大利卡塔尼亞大學(xué)工程博士學(xué)位。1994年始,他在意法半導(dǎo)體和德克薩斯農(nóng)工大學(xué)做過(guò)研究工作。后在德州儀器做過(guò)數(shù)據(jù)轉(zhuǎn)換器IC設(shè)計(jì),并擔(dān)任過(guò)國(guó)家半導(dǎo)體(美國(guó))設(shè)計(jì)總監(jiān)。自2010年起,他擔(dān)任ADI公司高速數(shù)據(jù)轉(zhuǎn)換器工程總監(jiān)。他曾連續(xù)7年擔(dān)任ISSCC數(shù)據(jù)轉(zhuǎn)換器技術(shù)小組委員會(huì)委員。他先后擔(dān)任過(guò)《IEEE電路與系統(tǒng)論文集》的副編輯、副主編和主編。他已撰寫或合作撰寫60篇論文及3本著作(其中最著名的是2011年劍橋大學(xué)出版社出版的《高級(jí)數(shù)據(jù)轉(zhuǎn)換器》),并擁有15項(xiàng)美國(guó)專利(及相應(yīng)的歐洲和日本專利)和其他申請(qǐng)中的專利。他還是多個(gè)科學(xué)獎(jiǎng)項(xiàng)的獲得者,包括英國(guó)盧瑟福阿普爾頓實(shí)驗(yàn)室的1995年CEU獎(jiǎng)、1999年IEEE電路與系統(tǒng)杰出青年作者獎(jiǎng)、2007年IEEE歐洲固態(tài)電路會(huì)議最佳論文獎(jiǎng)。他是IEEE院士(自2016年起)、IET院士(自2009年起)、Sigma Xi會(huì)員以及IEEE電路與系統(tǒng)協(xié)會(huì)理事會(huì)成員(2016 – 2018)。

 粵公網(wǎng)安備 44030902003195號(hào)
粵公網(wǎng)安備 44030902003195號(hào)