本文的試驗會引用兩家不同廠商的頻譜分析儀的功率測量結果。但是本文的結論對任何使用“后處理平均方法”的頻譜分析儀都適用。

第一個錯誤觀點：對均方根功率求平均，可以得出跨度為零的軌跡(或其一部分)的平均功率。為了更好的駁斥這個觀點，有必要先了解一下平均的數學定義。如公式1所示：MAVE是某個試驗N次測量的平均值，其中Mi是每一次測量的結果。

在這個例子中，儀器A和儀器B的結果，可接受的差異在一定范圍之內(比如±1dB)，所有的測試都是在頻率跨度為零ZS(zero span)的情況下測試的，這時頻譜分析儀會在一個固定的頻點，測量這個頻點的功率隨時間變化的關系。這里并不是刻意選擇ZS模式的，其實平均問題在傳統的頻域掃描測試中也存在。

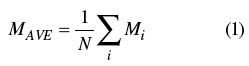在兩個例子中，都采用ZS模式測量零信道功率比ACPR(adjacent-channel-power-ratio)。對于現代采用數字中頻濾波器的頻譜分析儀而言，這種測量功能是必備的，可以在偏離載波中心不同頻偏的頻率點多次測量功率，而不需要重新調諧頻譜分析儀的中心頻率。

圖1顯示的是ZS模式下，一個GSM時隙脈沖信號。其中藍色的曲線是脈沖的功率包絡。這里測量的是“射頻輸出調制譜”，也就是所謂的ACPR測量。

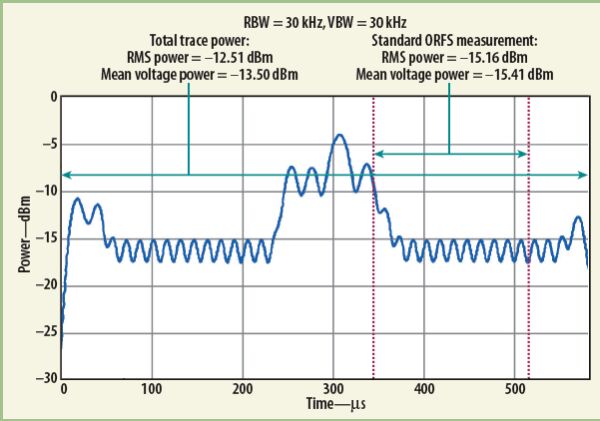從這條曲線可以得到很多結果，如最大峰值功率、最小功率和平均功率，尋找最大/最小功率在概念上非常直觀，儀器直接從軌跡中搜索出最大/最小點即可。

計算平均功率最簡單的方法(當然也是正確的)就是對紅色界限范圍內的測量點求平均。如公式2所示，其中N是紅色界限內的點數，Pith point是第i個點的功率。

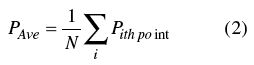問題是，儀器廠商對于功率平均的方法是不一致的。其中一個廠家是按照公式2來計算的；但是另一個廠商先把功率轉換成電壓，對電壓求平均，再把平均電壓換算成平均功率，如公式3所示。

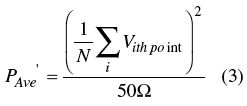由于兩種儀器輸出的平均值的差別不大，所以很難看出其中一種儀器用的是公式2，而另一種用的是公式3。有必要從兩種儀器分別取出多組軌跡，進行平均直到找到吻合之處。在圖1的例子中，采用“真正的均方根”平均功率算法(后面簡稱RMS功率)的儀器，和采用“電壓平均”功率的儀器之間的結果相差0.25dB(前者比后者高0.25dB)。這點差異可能會被簡單的認為是儀器之間的個體差異。盡管0.25dB看起來很小，但是當要求的精度僅僅是±1dB時，0.25dB就顯得有點大了。如果是測量整個脈沖的平均功率的話(調制譜測量的是脈沖50%到90%時間內的功率)，這個差異會擴大到約1dB。這個值就會接近我們所要求的儀器之間誤差容限了。

“電壓平均”功率代表的是“先平均再平方(mean-squared)”的功率(如公式3)，而“均方功率”則是“先平方再平均(mean-square)”功率。由統計學的知識我們可以得出：兩者的差就是幅度變化。也就是說，兩種儀器輸出功率的差值就是幅度變化。而且“均方功率”永遠大于“電壓平均功率”(RMS power > average voltage power)。

第二個關于功率平均的錯誤觀點就是：對功率求平均總是在線形單位(瓦特)下進行的。實際上很多儀器常常采用對數平均。同樣采用上面那個例子，假設測試中噪聲影響很大，為了去除噪聲，決定測量多組軌跡，對軌跡求平均。GSM標準規定，ORFS調制譜的測量需要對200個脈沖求平均。公式4是對應的計算公式，其中PTrace i是用公式2或公式3計算出的單條軌跡的平均值。

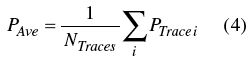當然對這個功率的線性表達結果(單位為瓦特)求平均是合理的，但是很多儀器提供了對數平均功能。這個例子中，以dBm為單位的功率進行了平均。例如，求 1和 3dBm的平均值：如果用線性平均結果為：(1.25mW 2mW)/2=1.62mW= 2.11dBm；但是對數平均的結果為：(1dBm 3dBm)/2=2dBm。因此對數平均的結果會引入0.11dB的誤差。

需要注意的是，對數平均引起的誤差的大小和信號是否重復有關。盡管對數平均方法是錯誤的，但是對于重復信號，對數平均和線性平均的結果一致。需要注意，這里說的重復信號指的是每一個周期，其功率對時間關系是完全一樣的。

必須要牢記：非重復信號會引入誤差，如果不注意，經常會導致實驗室的測量數據和實用環境中的誤差很大。因為在實驗室中，我們通常采用很好的“任意波形發生器ARB(arbitrary waveform generator)”作為信號源，這種源通常是把一個波形不斷的重復播放。但是實用環境中的信號肯定不是重復性的。然而，只要不同周期之間的功率差別不是很大，對數平均和線性平均的誤差也不會很大。

另一個需要注意的是，軌跡平均時，每次測得的各條軌跡之間對應的“點和點”的平均算法問題。同樣的，信號的重復性會影響對數平均引起的誤差。在這里，軌跡上的每一個點和其他軌跡上的對應點一起求平均，得出的結果作為這個點的平均值。

同樣的，軌跡上的每一個點和其他軌跡上的對應點(同一個x軸)一起求平均，得出一條平均的軌跡線。這里x軸對應的是時間，當然對于頻率也適用。和前面一樣，這里可以采用線性平均或對數平均。這樣對x軸上每一個點都做完平均之后就可以得到一條平均軌跡了。如果信號是重復的，線性平均和對數平均的結果相同，因為x軸上每一個點的功率在各次測量的軌跡上是相同的。

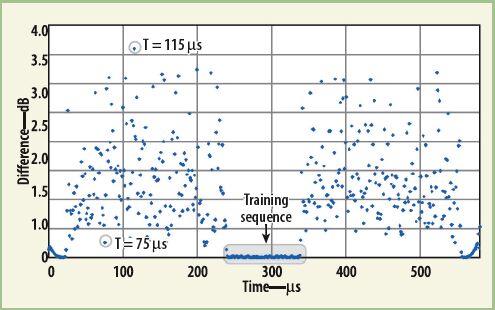
當被測信號不是重復的結果如何呢？圖2就是對20個不同的EDGE信號，分別采用對數平均和線性平均后的結果。當然兩條曲線會有差異，而且可以看出對數平均的結果比線性的小。圖3顯示的是兩條曲線每一個點的差異。注意，正如我們所料，訓練序列(譯者注：用于同步和信道估計的部分，是完全重復的)部分的軌跡完全重合。

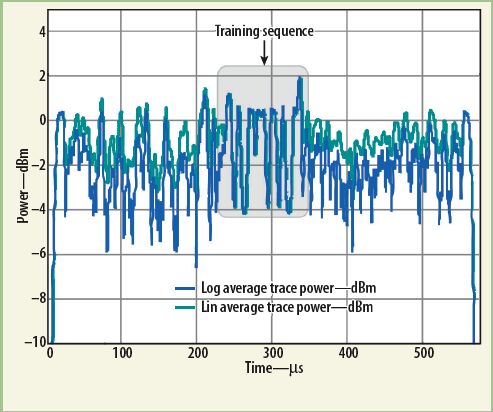這些差異源于對數平均會放大功率的抖動，這個道理可以通過一個簡單的例子描述：假設在某個特定的時間點(或者頻點)反復測量N次功率值，功率在0dBm和-10dBm之間抖動，其中一半的讀數為0dBm，而另一半為-10dBm，即“峰-峰”差值為10dB。如果用對數平均，其結果為-5dBm。但是如果用線性平均，要先把0dBm和-10dBm轉為瓦特，然后求平均，最后再把瓦特轉換為dBm，其結果是0.55毫瓦，即-2.6dBm。因此采用對數平均的誤差高達2.4dB。

眾所周知，對數單位變化xdB，對應的線性功率變化為10(x/10)倍。因此可以用下面的公式得到正確值，假設一半的功率讀數為Mhi，另一半的讀數比剛才低ΔdB。

注意：隨著Δ增加到無窮大，10log[(1 10-Δ/10)/2]這一項的數值趨向于-3dB。也就是說，如果兩種功率出現的次數相等的時候，較高的功率最多比線性平均功率高3dB。還可以進一步把這個結果推廣到任意的功率出現比例。

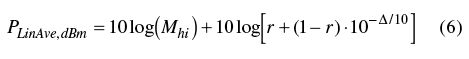公式6中，r是高功率值(Mhi)出現的比例，當Δ趨向于無窮，平均功率最多比高功率小10log(r)倍。

當然，也可以推導出多數平均的結果

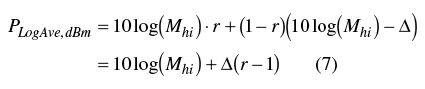如果公式7減去公式6，其結果就是線性平均和對數平均的差異(即對數平均引入的誤差)

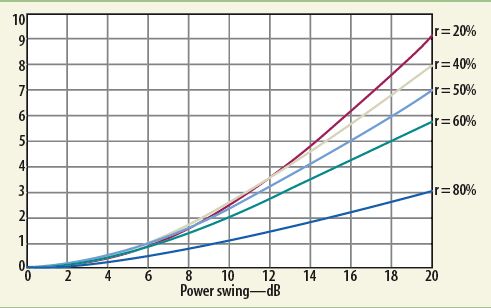
圖4描述的是公式8的結果(對數平均的誤差)隨著Δ變化的關系，其中r是參變量。這張圖的Δ只算到20dB，因為一般信號的峰均比都不會超過這個值。

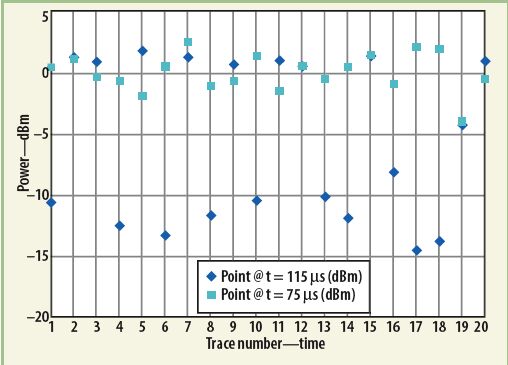
作為檢驗，有必要參考一下實際測試的數據(參見圖3)。這幅圖中有兩個點被標出，一個是差異較大的點(差別大于3.5dB，T=115μs))，另一個是差異很小的點(約0.25dB，T=75μs)。根據前面的討論，很容易理解在“功率對時間”的圖形中，這些點的位置肯定不一樣，誤差大的點的擺幅比較大，而誤差小的點的擺幅也相應的很小。這可以從圖5中看出。

圖5中，在T=115μs的這個點的擺幅高達約15dB，而在T=75μs的這個點，擺幅約5dB。假設高、低功率出現的次數相同(即r=0.5)，這T=115μs的這個點的擺幅約4.5dB，而T=75μs的這個點，擺幅約0.5dB(參見圖4和公式8)。上述數字比實測的3.5dB和0.25dB,要高一些，因為圖4所示的是最壞情況(即只有兩種功率讀數，且出現機率相同)，由于實際情況下，不止只有兩種功率讀數，所以實際結果要略小一些。

總而言之，工程師應該記住并不是所有的頻譜分析儀輸出的平均功率結果都是正確的。而且其誤差的程度和被測信號有關，因此必須注意以下事項：

* 了解頻譜分析儀計算平均功率的方法是RMS方法還是“電壓平均”方法
* 功率應該在線性單位(瓦特)下進行平均，但是有些儀器會提供對數平均
* 重復信號對于理解對數平均的誤差可能有誤導作用。其結果要么是固定誤差(例如RMS功率和電壓平均功的誤差為恒定值)，要么就沒有誤差(例如對數平均和線性平均的結果相同)

不同的平均方法導致的誤差可能到達1dB以上。理解儀器如何平均的的最好方法是，取出幾條軌跡的數值，手工(編程)求其平均值，判斷儀器輸出結果是否和手工計算的相同。盡管這項工作比較麻煩，但是對于高精度的功率測量來說，這個工作還是有必要的。