快速傅里葉變換(FFT)實現了時域到頻域的轉換，是信號分析中最常用的基本功能之一。FFT變換時，總是從離散數據中選取一部分處理，將其稱為一幀數據。而且FFT是在一定假設下完成的，即認為被處理的信號是周期信號。因此，FFT之前會對這一幀數據進行周期擴展。

以CW信號為例，如果選取的這一幀數據不是信號周期的整數倍，則在周期擴展時會存在樣點的不連續性，如圖1所示。這將導致FFT之后得到的頻譜失真，主要體現在頻率成分上。理論上，頻譜中只包含待測信號的頻率，但實際上此時的頻譜包含眾多的頻率分量。通常將這種現象稱為頻譜泄露效應。

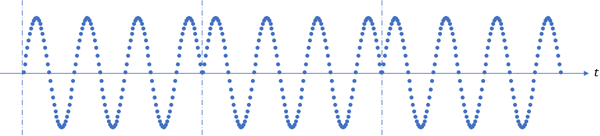
圖1. 周期擴展造成樣點不連續

為了抑制頻譜泄露效應，可以采用諸如Hanning、Kaiser等多種時間窗。還有一種特殊的時間窗——矩形窗，其實就是不加時間窗，直接對原始樣點做FFT變換，上述例子就是采用矩形窗的情況。只有采用矩形窗，而且窗寬度不是信號周期的整數倍時，才會發生明顯的頻譜泄露效應。

本文的重點并非介紹如何采用時間窗抑制頻譜泄露效應，而是從理論上剖析采用矩形窗時造成頻譜泄露的本質。

1. 為什么會造成頻譜泄露？

圖1所示的樣點不連續也意味著相位不連續，存在180°相位反轉。總體來講，可以將其理解為相位調制，而且是一種特殊的相位調制，調制信號不是經典的正弦波信號，而是方波信號，可以將調制信號寫為如下形式：

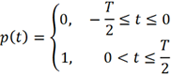
式中，T 為調制信號的周期，為一幀波形時長的兩倍。這意味著在t=0 時刻，載波的相位發生了變化。

既然可以理解為相位調制，則可將已調信號寫為如下形式：

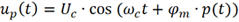
式中φ_m為相位偏移，對于圖1的例子，φ_m=π。很顯然，調制信號已經不再是單頻點信號，而是多頻點信號。對于圖2所示的周期為T 的方波信號，其頻譜包含DC、基波及其眾多的奇次諧波分量 。

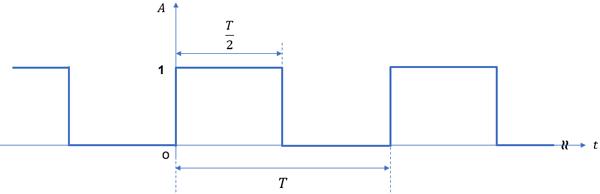
圖2. 調制信號p(t)的時域波形

滿足Dirichlet 條件時，任何周期函數均可以進行傅里葉級數展開，p(t) 可以寫為：

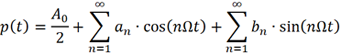
式中，Ω為方波信號的基波頻率，Ω=2π/T。

經過計算，可以得到a_n 和b_n 如下：

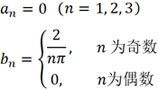
這意味著p(t) 只包含DC、基波及其奇次諧波，但階數越高，諧波強度越弱。

可以將p(t) 重新寫為：

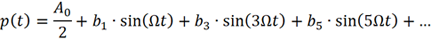
為簡便起見，首先考慮調制信號只包含DC和基波的情況，這又回到經典的相位調制。

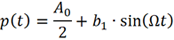
將其代入已調信號u_p (t) 后可得

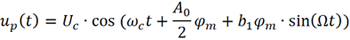
上式可以寫為復指數形式

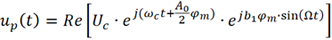
為了進一步分析，可將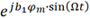進行傅里葉級數展開，其展開式為宗數為b₁φ_m的第一類貝塞爾函數：

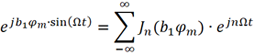
將其代入復指數表達式

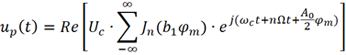
則u_p (t) 可重新表示為

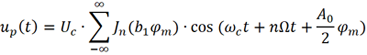
可以看出，當只考慮調制信號的DC和基波時，已調信號u_p (t)將包括ω_c及ω_c+nΩ(n為整數) 等眾多頻率分量。

實際中調制信號還包含豐富的諧波分量，因此對載波進行相位調制后的頻譜更加豐富。面對的困難是，考慮的諧波越多，公式推導越復雜。為了簡化，下面只考慮到3次諧波。

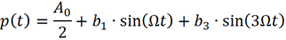
對應的已調信號為

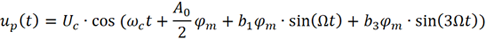
類似地，可以寫為如下復指數形式

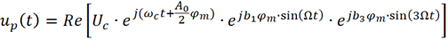
將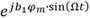、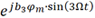分別進行傅里葉級數展開為

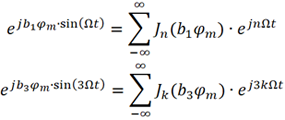
經過一番推導可得

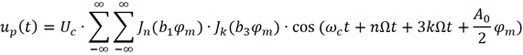
由此可見，當考慮到調制信號的三次諧波時，已調信號u_p (t) 的頻譜更加豐富，包括ω_c、ω_c+nΩ 、ω_c+3kΩ及ω_c+nΩ+3kΩ(n,k為整數) 等眾多頻率分量。

以此類推，當考慮p(t) 更高階的諧波時，將會有更多的頻率項，但是從頻率上看，各個頻率分量都是均勻分布的，而且相鄰譜線之間的間距始終為基波Ω。

2. 下面討論一下u_p (t) 主要頻率分量的幅度。

(1) 首先考慮載波ω_c的幅度，以上面考慮到三次諧波的情況為例。當nΩt+3kΩt=0 時，對應的就是載波分量。這要求n=-3k (k 為整數)，此時可以得到：

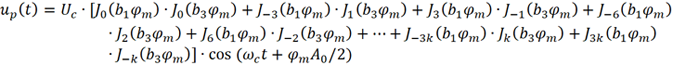
對于第一類貝塞爾函數J_n (x)，其奇偶特性如下：

當n 為奇數時，J_n (x) 為奇函數；當n 為偶數時，J_n (x) 為偶函數。

進一步化簡可得

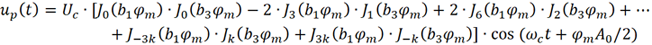
因以上考慮的都是相位偏移 φ_m=π的情況，故b₁φ_m=2，b₃φ_m=2/3，代入上式得

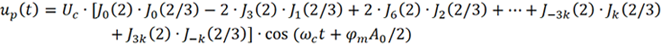
對于第一類貝塞爾函數，J_n (2)=J_n (2/3)=0 (n≥5)，則

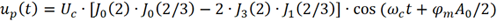
根據第一類貝塞爾函數，上式計算得到的載波信號幅度非常微弱。

(2) 頻率分量ω_c+Ω的幅度分析。當n=-3k+1 時，對應的就是ω_c+Ω頻率分量。

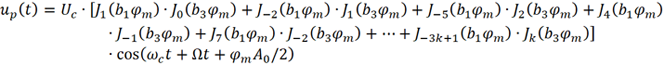
由于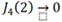，且J_n (2)=J_n (2/3)=0 (n≥5)，上式進一步化簡得

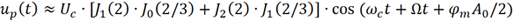
該頻率分量的幅度要遠遠大于載波的幅度！

(3) 頻率分量ω_c-Ω的幅度分析。當n=-3k-1 時，對應的就是ω_c-Ω頻率分量。

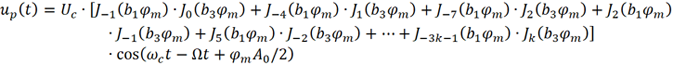
由于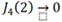，且J_n (2)=J_n (2/3)=0 (n≥5)，上式進一步化簡得

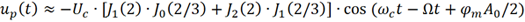
該頻率分量的幅度也遠遠大于載波的幅度！

而且對比 ω_c+Ω 和 ω_c-Ω 兩個頻率分量，它們的幅度相同！也就是說，從頻譜上看，它們是關于載波對稱的！

(4) 頻率分量ω_c+2Ω 的幅度分析。當n=-3k+2 時，對應的就是ω_c+2Ω 頻率分量。

雖然(n,k) 的組合很多，但是當階數較大時，J_n (2)= J_n (2/3)=0 (n≥5)，因此可得

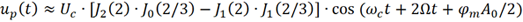
經過計算，該頻率分量的幅度非常微弱。

(5) 頻率分量ω_c-2Ω 的幅度分析。當n=-3k-2 時，對應的就是ω_c-2Ω 頻率分量。

雖然(n,k) 的組合很多，但是當階數較大時，J_n (2)= J_n (2/3)=0 (n≥5)，因此可得

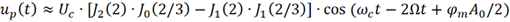
該頻率分量與ω_c+2Ω 的幅度相同，依然非常微弱。

上面從理論上解釋了頻譜泄露的起因，而且當發生頻譜泄露時，會產生眾多的、分布均勻的頻率分量，相鄰譜線的頻間距取決于FFT時一幀波形的時長。

值得一提的是，相位偏移 φ_m不僅對各個頻率分量的幅度有影響，也會影響頻率分布，以后有機會再來解釋這一點。

3. 通過使用AWG播放一個CW信號驗證上述推導。

使用AWG 輸出一個100MHz 頻率的CW 信號，波形時長為10.5個周期，如圖3所示，當循環播放時便可以模擬上述的相位不連續性，會造成180°的相位跳變。

對于這種波形時長不是信號周期整數倍的情況，當單次播放時，信號的頻率就是100MHz ，但是當連續播放時相當于引起了相位調制，按照上述理論分析，頻譜中將包含很多頻率成分，圖4給出了信號的實測頻譜。

本例中，波形時長為105ns，這意味著頻譜中相鄰譜線之間的頻率間隔約為：4.76MHz，這與圖4所示的頻譜是吻合的。

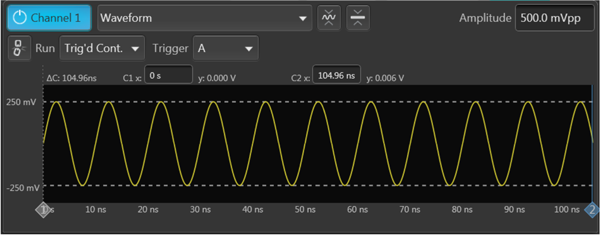
圖3. 波形時長為10.5個信號周期

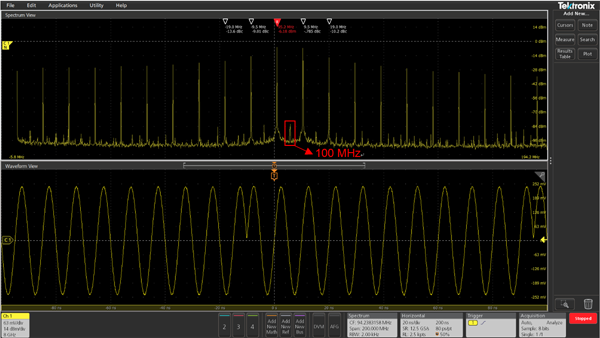
圖4. 時域波形及其頻譜

小結

對于使用矩形窗進行FFT時可能存在的頻譜泄露效應，本文從理論上定性地進行了分析。究其原因，是因為當進行周期擴展時造成了相位的不連續。相位的不連續可以當作相位調制來處理，經過一系列推導最終解釋了為什么會出現眾多的頻率成分。文中還對特定相位偏移情況下的頻率分量的幅度進行了分析。文末通過一個實例模擬了這種相位不連續，并測試了波形和頻譜，實測結果與理論推導相吻合。