眾所周知，選擇示波器時經常會用到5倍法則，其實不僅僅是針對帶寬，當涉及到快沿信號上升時間測試時，根據上升時間選擇示波器也會用到5倍法則。本文將分別對這兩種情況下的5倍法則展開討論，并介紹當考慮示波器和探頭構成的整個測試系統時又該如何選擇。

1. 示波器帶寬選擇時的5倍法則

所謂5倍法則，就是為了保證信號的幅度測試精度，示波器的帶寬至少要選擇為信號頻率的5倍！這通常針對于正弦波信號，因為其頻譜只有一根譜線。而對于脈沖信號，由于理論上具有無數個諧波，通常將示波器帶寬選擇為所關注的最高次諧波頻率的5倍。

為什么按照5倍法則選擇示波器的帶寬呢？如果不按照這個法則，對于信號幅度測試精度有多大影響呢？選擇示波器帶寬時，5倍法則主要適用于哪一類示波器？

為了解釋這些問題，首先需要了解一下示波器的模擬帶寬。示波器的模擬通道具有低通濾波器的頻率響應，帶寬就是指該低通濾波器的3dB截止頻率。如果測試一個頻率與示波器標定帶寬相同的正弦波信號，電壓幅度測試結果將下降為真實電壓值的0.707倍，如果用對數表示，則測量幅度將降低3dB。

可將示波器的模擬通道等效為一個RC低通濾波器，為了簡便起見，此處只考慮一階RC低通濾波器，其等效電路及幅頻響應如圖1所示。一階RC低通濾波器的幅頻響應表達式可寫為：

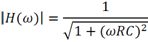
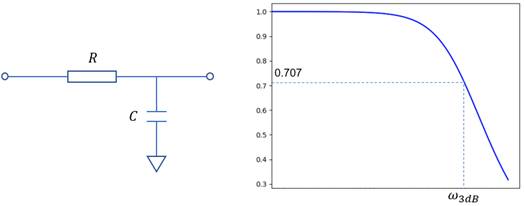
圖1. 一階RC低通濾波器電路模型及其幅頻響應

使得傳輸系數下降至0.707時的頻率稱為低通濾波器的截止頻率，或者稱為3dB帶寬，據此可得

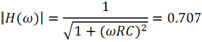
經計算得

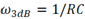
代入幅頻響應函數后得

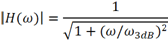
由圖1中的幅頻響應可知，隨著頻率的不斷提高，信號經過濾波器時的衰減越大，這也意味著測得的信號幅度誤差越大。如何保證信號的幅度測試精度呢？

很明顯，當示波器的帶寬遠遠大于信號的頻率時，才可以得到非常高的幅度測試精度。但是，示波器帶寬越大，成本越高，實際選擇時必須折中考慮成本和測試精度。業界通常采用5倍法則選擇示波器的帶寬，此時可以保證至少98%的幅度測試精度。

假設待測正弦波信號的幅度為1V，角頻率為ω₀，當測試精度不低于98%時，則滿足如下關系式

進一步化簡可得

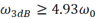
這表明，當測試正弦波信號時，只有在示波器的帶寬不低于正弦波信號頻率的4.93倍時，才能保證至少98%的測試精度。為了方便，通常建議示波器帶寬至少為信號頻率的5倍，這就是5倍法則的由來。

表1. 測試不同頻率的正弦波時對應的幅度精度

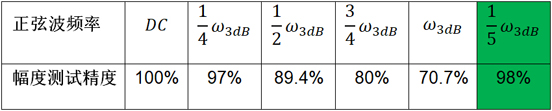
至于是否按照5倍法則選擇示波器的帶寬對測試精度有多大影響，在示波器帶寬固定的情況下，表1給出了不同頻率的正弦波信號對應的理論測試精度。顯然，示波器帶寬相對于信號頻率越大，幅度測試精度越高！

選擇示波器時必須要遵循5倍法則嗎？可以肯定的是，帶寬大是有好處的，尤其是針對于經濟型的示波器而言(BW≤1GHz)。因為通常并不會對這類示波器的頻率響應做相應補償，其幅頻響應平坦度并不好。而且，這類示波器模擬通道基本就是1階RC低通濾波器的頻響，如果要求98%的測試精度，就要按照5倍法則選擇示波器帶寬。

而對于中高端示波器，示波器內部通常都引入了模擬通道的補償算法，可以得到比較平坦的幅頻響應，因此，對于這類示波器可以不按照5倍法則進行選擇。值得一提的是，對模擬通道的補償并不會擾亂測試，相反，可以大大改善測試效果，提高信號保真度，尤其是針對于寬帶信號以及高速數字信號的測試，這種補償是至關重要的。

2. 示波器結合探頭使用時，測試系統的帶寬如何確定？

前面介紹了選擇帶寬時5倍法則的由來，接下來介紹當示波器結合探頭使用時，整個測試系統的帶寬由誰決定，并為下一步推導上升時間的級聯公式做準備。

與示波器的模擬通道類似，探頭也呈現為低通濾波器的頻率響應。很明顯，當示波器帶寬遠遠大于探頭帶寬時，系統的帶寬取決于探頭；當探頭的帶寬遠遠大于示波器的帶寬時，系統的帶寬取決于示波器。

通常認為，測試系統的帶寬和示波器及探頭的帶寬滿足如下關系：

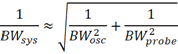
其實，當示波器帶寬和探頭帶寬相當時，采用這個公式計算得到的系統帶寬的誤差是比較大的。示波器和探頭構成的測試系統的幅頻響應表達式為

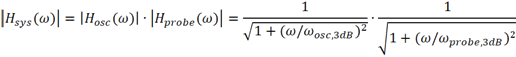
類似地，當系統的傳輸系數下降至0.707時的頻率即為系統的3dB帶寬，這意味著

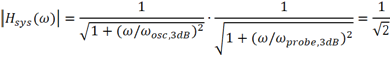
化簡可得

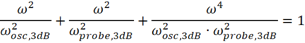
如果將上式中的高次項忽略，則便可以得到上面的結論。

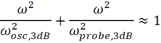
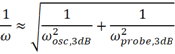
那么能否將高次項忽略呢？當示波器帶寬和探頭帶寬差異較大時，高次項相對較小，是可以忽略的。二者帶寬越接近，則忽略高次項帶來的誤差越大，當二者帶寬相同時，使用上式計算的系統帶寬的誤差最大，可以達到25%的誤差。但可以肯定的是，總體的系統帶寬是小于示波器和探頭帶寬的！

盡管如此，對于中高端示波器和有源探頭而言，由于可以對探頭和模擬通道的頻響做補償，因此即使二者帶寬相同，也可以滿帶寬使用。比如，示波器帶寬為16GHz，探頭帶寬也為16GHz，則系統帶寬也可以達到16GHz。而經濟型示波器卻沒有這種補償頻響的功能，系統帶寬會變窄，使用時要特別注意。

3. 按照上升時間選擇示波器時的5倍法則

本節將首先介紹帶寬與上升時間的關系，并給出理論推導；然后著眼于示波器和探頭構成的整個測試系統，描述了系統的上升時間與示波器和探頭的上升時間有著怎樣的關系；最后道出結論，為了提高測試精度，建議采用5倍法則進行選擇。

對于任意一個LTI (線性時不變)系統，當施加一單位階躍信號時對應的零狀態響應稱為單位階躍響應(簡稱為階躍響應)，該過程可以理解為其瞬態響應過程，響應的快慢取決于系統帶寬，一般使用上升時間衡量。系統帶寬越大，則瞬態響應速度越快，上升時間也越短。對于示波器和探頭，亦是如此。

示波器和探頭的上升時間與帶寬之間具有怎樣的量化關系？

示波器的模擬通道和探頭均呈現為低通濾波器的特性，為了便于推導，此處假設二者均具有一階RC低通濾波器的頻響。

如果要確定上升時間，則需要從階躍響應入手，一階RC低通濾波器的階躍響應為

式中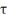，為濾波器的時間常數，且.

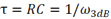如果按照10%~90%的規則定義上升時間，則可以按照如下方法進行計算。

在t=0時刻，信號電壓為0.

假設t₁時刻，信號電壓上升至0.1 V，則滿足：。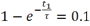

假設t₂時刻，信號電壓上升至0.9 V，則滿足：。

經計算可得上升時間為：

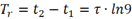
進一步化簡得

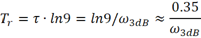
對于低通濾波器而言，3dB截止頻率即為3dB帶寬，因此可以得到關于帶寬與上升時間關系的經典公式：

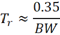
該公式是基于一階RC低通濾波器頻響推導的，對于BW ≤ 1GHz的示波器和探頭而言，基本都適用。如果是更高帶寬的中高端示波器和探頭，其通道依然相當于低通濾波器，但通常并不是一階低通濾波器的頻響，所以上述公式中的系數不再是0.35，而是位于0.4~0.45之間。

對于示波器和探頭構成的測試系統，總體的上升時間如何推算呢？

前面已經介紹了測試系統帶寬與示波器和探頭帶寬之間的關系，結合帶寬與上升時間的關系，則整個測試系統與示波器和探頭的上升時間滿足：

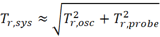
也就是說，整個測試系統的上升時間惡化了。

對于待測的快沿信號而言，定義其等效3dB帶寬為BW_signal，與上升時間也可以近似等效于上面的關系式。如果使用示波器和探頭測試該快沿信號，則信號等效3dB帶寬的測量值與測試系統的帶寬近似滿足如下關系：

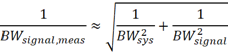
再根據帶寬與上升時間的關系，將上式進一步化簡得

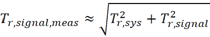
由此可見，實際測量的快沿信號的上升時間與系統的上升時間有很大關系。

通常推薦測試系統的上升時間不大于待測信號上升時間的1/5，以提高測試精度，這就是在快沿測試過程中的5倍法則！

表2. 不同的系統上升時間對應的測試誤差

表2給出了測試某一快沿信號時，不同的系統上升時間對應的測試誤差。系統上升時間相對于信號上升時間越小，則測試誤差越小，測試精度越高。當系統上升時間為信號上升時間的1/5時，測試精度可以達到98%。這也是在該測試場景下使用5倍法則的原因！

為了進一步驗證，分別將示波器的帶寬限定為1GHz、500MHz和200MHz，測試同一快沿脈沖信號的波形如圖2所示。當帶寬不足時，測試系統上升時間增大，嚴重惡化了測試精度。

圖2. 帶寬分別限定為1GHz、500MHz和200MHz時測試同一快沿信號的結果

小結

本文描述并解釋了在選擇示波器時常用的5倍法則，該法則不僅適用于示波器帶寬的選擇，也適用于測試快沿信號時系統自身上升時間的選擇。對于級聯系統的等效帶寬和上升時間，文中亦有描述。為了提高幅度和上升時間測試精度，強烈推薦采用5倍法則選擇示波器。