如何理解相位噪聲與時間抖動的關系?
每當介紹相位噪聲測試方案時,都會提到時間抖動,經(jīng)常提到二者都是表征信號短期頻率穩(wěn)定度的參數(shù),而且是頻域和時域相對應的參數(shù)。正如題目所示,相位噪聲與時間抖動有著一定的關系,那么相噪是與哪種類型的抖動相對應,彼此之間又有著怎樣的數(shù)學關系,這些疑問都將在文中找到答案。
1. 相位噪聲與時間抖動概述
相位噪聲通常是針對CW信號而言的,是表征信號頻譜純度的非常重要的參數(shù),衡量了信號頻率的短期穩(wěn)定度。相位噪聲是頻域的參數(shù),在時域還有一個與之對應的參數(shù)——隨機抖動,二者之間存在一定的數(shù)學關系,可以相互轉(zhuǎn)換。
在前面關于相位噪聲測試的文章中,給出了IEEE早期關于相噪的定義,同樣的,關于時間抖動,SONET規(guī)范也給出了相應的定義:
“Jitter is defined as the short-term variations of a digital signal’s significant instants from their ideal positions in time”.
抖動定義中給出了三個要素:
(1) significant instants,通常是指信號的上升沿或者下降沿;(2) ideal positions in time,這是指信號上升沿或下降沿在時間維度上的理想位置;
(3) short-term variations,信號實際上升沿或下降沿相對于理想位置時間偏移的短期波動。
雖然定義中只提到了數(shù)字信號,但實際上具有普遍適用性,當然對于CW信號也是適用的。
上述定義所給出的是一種綜合性抖動,按照不同的原因機制,又可以分解為多種不同的抖動分量,包括:隨機抖動,周期性抖動,數(shù)據(jù)相關抖動,占空比失真等。
CW信號可以理解為一種特殊的數(shù)字碼流信號,理論上只有隨機抖動和周期性抖動這兩種分量。隨機抖動是由寬帶噪聲引起的,周期性抖動是由串擾引起的,從產(chǎn)生機制上講,都相當于對信號進行了調(diào)頻或者調(diào)相。
高端的頻譜儀及專業(yè)的相噪測試設備,除了能夠給出相位噪聲,還可以測試載波附近的spur。根據(jù)產(chǎn)生的機制可以判定,相位噪聲是與隨機抖動相對應的,spur是與周期性抖動相對應的。
下文主要聚焦在相噪與隨機抖動的關系,后面所提到的抖動,除非特別說明,否則一律視為隨機抖動。
2. 相位噪聲與時間抖動有何關系?
理想的CW信號用公式可以表示為
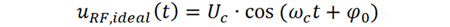
相位噪聲可以理解為寬帶隨機噪聲對CW信號的相位調(diào)制,因此,CW信號的頻譜具有對稱的左右兩個邊帶。
從相位調(diào)制的角度看,經(jīng)寬帶隨機噪聲u(t) 調(diào)制后,已調(diào)信號可以表示為

式中,kPM為調(diào)相比例系數(shù),u(t) 為寬帶隨機信號,通常可以視為白噪聲信號,相當于由無數(shù)個點頻信號疊加而成。
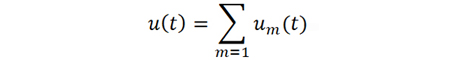
對于u(t) 中包含的任意頻點?m,對應的調(diào)制信號表達式為
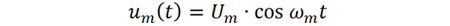
下面以頻率為?m 的信號作為調(diào)制信號,從數(shù)學的角度推導單邊帶相位噪聲與時間抖動的關系。
對射頻載波調(diào)相后,已調(diào)信號的表達式為
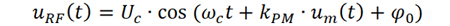
由調(diào)制信號引起的載波信號的瞬時相位定義為
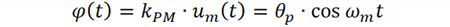
通常稱θp 為調(diào)相因子,表征了載波信號相位波動的最大偏移,單位為弧度rad.,其表達式為
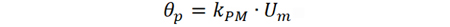
因此,已調(diào)信號又可以寫為
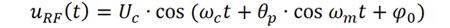
將上式展開為

因?qū)拵г肼暦确浅P。瑢d波信號進行相位調(diào)制造成的相位偏移也是非常小的,通常θp<<1,則存在如下近似關系:
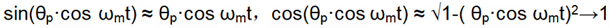
上式可進一步寫為
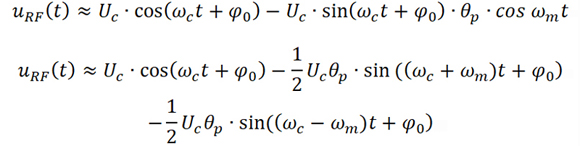
理論上,如果使用單頻點信號作為調(diào)制信號對射頻載波進行相位調(diào)制,已調(diào)信號可以展開為第一類貝塞爾函數(shù),從展開式可以看出,頻譜分量非常豐富,而且關于載波頻率左右對稱。而上面的公式表明,卻只有載波、左右邊帶三個頻率分量,這正是因為上面做了一些數(shù)學近似。
以右邊帶為例,其信號功率為
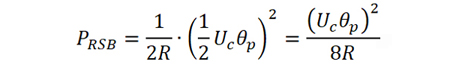
載波信號功率為
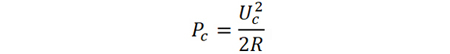
則在頻偏fm=?m/2π 處的單邊帶相位噪聲為
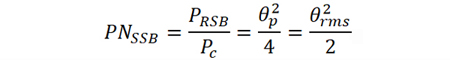
式中,θrms為載波信號相位波動的有效值。該公式具有普遍適用性,適用于任意頻偏。
相位噪聲表征了某一頻偏處的單邊帶相對噪聲功率譜密度,由上式可知,θ2rms表征了雙邊帶相對噪聲功率譜密度。
上面是以寬帶隨機噪聲中的任意單頻點信號作為調(diào)制信號為例,簡要描述了相位噪聲的形成,而寬帶噪聲包含無數(shù)個單頻點信號,對載波進行相位調(diào)制后,那么從頻譜上看,同樣可以得到左右對稱的兩個邊帶,而且左右邊帶的頻譜是連續(xù)的。
隨機抖動與相位噪聲有什么關系呢?
時間抖動就是指載波信號上升沿或者下降沿在時間軸上的短期波動,隨機抖動是由于寬帶噪聲引起的邊沿無規(guī)則隨機波動,這與相位噪聲是一一對應的,邊沿的波動是各個頻偏處相噪的綜合體現(xiàn)。載波邊沿的隨機波動,存在一個波動范圍,從概率密度上講,基本服從高斯分布,通常采用標準差表征隨機抖動,這也是隨機抖動的有效值,也是通常要測試的參數(shù)。
時間抖動引起了相位的波動,只要確定了相位波動的量,那么也就確定了時間抖動。
將各個頻偏處的相位噪聲求和并進一步變換可得
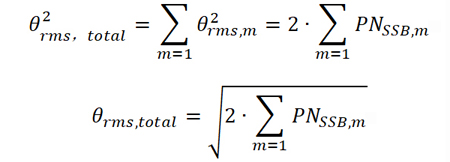
由于相位噪聲的邊帶是連續(xù)的,因此,上式可以用積分表示
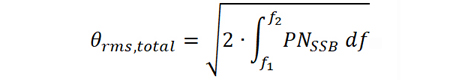
當然,測試設備是沒有辦法進行積分的,只能對離散的測試數(shù)據(jù)進行求和來模擬積分的效果。
θrms,total 即為由總體的相位噪聲引起的相位波動,結合載波頻率并運用如下公式便可以計算出對應的時間抖動
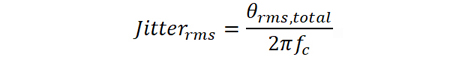
值得一提的是,上述公式中的相位噪聲不是對數(shù)值,而是線性值!而且,根據(jù)相位噪聲計算得到的抖動為隨機抖動,換言之,隨機抖動與相位噪聲是一一對應的。
3. 如何測試時間抖動?
從目前看,關注時間抖動的信號主要分為兩類:快沿信號和CW信號。前者通常是指在高速串行總線通信中的比特流信號及其時鐘信號,這類信號普遍具有非常快的邊沿,頻譜分量較為豐富。后者主要是指諸如射頻載波、晶振信號等單頻點信號,這類信號頻譜相對單一。
使用示波器是測試時間抖動最直接的方法,可以直接測試抖動,而不需要由相位噪聲推導而來,對于上述兩類信號都是適用的。尤其是對于快沿信號,不僅要測試各種抖動分量,還要測試幅度、邊沿時間以及眼圖等信號特征參數(shù),必須要使用示波器進行測試。
對于CW信號,基本上只關注隨機抖動,如果給出了抖動的指標要求,一定會給出對應的是哪個頻偏范圍。中高端示波器可以直接測試隨機抖動,而且支持設定積分頻偏范圍,觀測該頻偏范圍內(nèi)的總隨機抖動。但缺點是,示波器自身的抖動噪底往往較大,如果CW信號自身的隨機抖動與示波器抖動噪底相當,那么就無法直接準確測試了。
如前所述,由相位噪聲可以推導出隨機抖動,那么就可以先測試相位噪聲,然后再根據(jù)公式計算出隨機抖動。通過配置自動相噪測試選件,中高端頻譜儀測試相噪和抖動更加方便。而且單純從隨機抖動的測試能力而言,頻譜儀自身的抖動噪底也好很多,如果超出了頻譜儀的測試能力,還可以選擇測試相噪的“專家級”設備——信號源分析儀,相噪測試能力更強。優(yōu)點很明顯,但缺點也很明顯,這些頻域設備只能測試頻域相關參數(shù),卻無法進行時域相關測試!
無論是使用示波器直接測試隨機抖動,還是使用頻譜儀等設備先測試相噪、再計算隨機抖動,整個測試都是非常簡單、智能的。那么,應該如何選擇呢?關鍵還是取決于儀表自身的測試能力和功能是否滿足需求!
以上便是要給大家分享的內(nèi)容,希望對大家有所幫助~~
小文雖短但不乏精華,希望大家持續(xù)關注“微波射頻網(wǎng)”,后續(xù)精彩不斷~

 粵公網(wǎng)安備 44030902003195號
粵公網(wǎng)安備 44030902003195號