S參數(shù)是RF工程師/SI工程師必須掌握的內(nèi)容，業(yè)界已有多位大師寫過關于S參數(shù)的文章，即便如此，在相關領域打滾多年的人， 可能還是會被一些問題困擾著。你懂S參數(shù)嗎? 請繼續(xù)往下看...臺灣同行圖文獨特講解！

本文目錄 上：

1. 簡介：從時域與頻域評估傳輸線特性

2. 看一條線的特性：S11、S21

3. 看兩條線的相互關系：S31、S41

4. 看不同模式的訊號成份：SDD、SCC、SCD、SDC

5. 以史密斯圖觀察S參數(shù)

6. 仿真范例 -- 地回路有沒有slot對S11, S21的影響 -- 有效介電系數(shù)如何取得

7. 問題與討論

8. Reference

1、簡介：從時域與頻域評估傳輸線特性

良好的傳輸線，訊號從一個點傳送到另一點的失真(扭曲)，必須在一個可接受的程度內(nèi)。而如何去衡量傳輸線互連對訊號的影響，可分別從時域與頻域的角度觀察。

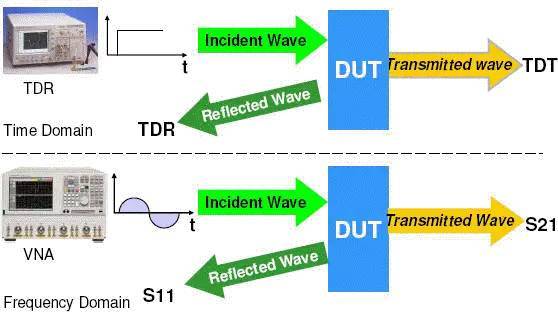
?S參數(shù)即是頻域特性的觀察，其中'S'意指'Scatter'，與Y或Z參數(shù)，同屬雙端口網(wǎng)絡系統(tǒng)的參數(shù)表示。

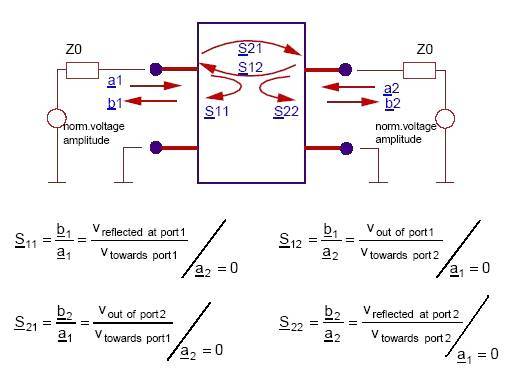
?S參數(shù)是在傳輸線兩端有終端的條件下定義出來的，一般這Zo=50奧姆，因為VNA port也是50奧姆終端。所以，reference impedance of port的定義不同時，S參數(shù)值也不同，即S參數(shù)是基于一指定的port Zo條件下所得到的。

2. 看一條線的特性：S11、S21

如下圖所示，假設port1是訊號輸入端，port2是訊號輸出端

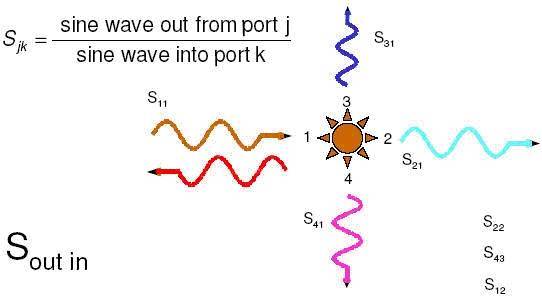
?S11表示在port 1量反射損失(return loss)，主要是觀測發(fā)送端看到多大的的訊號反射成份；值越接近0越好(越低越好 ，一般-25~-40dB)，表示傳遞過程反射(reflection)越小，也稱為輸入反射系數(shù)(Input Reflection Coefficient)。

S21表示訊號從port 1傳遞到port 2過程的饋入損失(insertion loss)，主要是觀測接收端的訊號剩多少；值越接近1越好(0dB)，表示傳遞過程損失(loss)越小，也稱為順向穿透系數(shù)(Forward Transmission Coefficient)。

3、看兩條線的相互關系：S31、S41

?雖然沒有硬性規(guī)定1、2、3、4分別要標示在線哪一端，但[Eric Bogatin大師]建議奇數(shù)端放左邊，且一般表示兩條線以上cross-talk交互影響時，才會用到S31。以上圖為例，S31意指Near End Cross-talk (NEXT)，S41意指Far End Cross-talk (FEXT).

4、看不同模式的訊號成份：SDD、SCC、SCD、SDC

以上談的都是single ended transmission line (one or two line)，接著要談differential pair結(jié)構(gòu)。

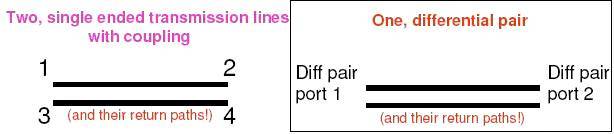
?5、以史密斯圖觀察S參數(shù)

因為S11、S22是反映傳輸線的reflection，不難理解S11其實也可以直接以反射系數(shù)表示。

?既然是反射系數(shù)，那就可以用史密斯圖來觀察了，史密斯圖可以想做是把直角坐標的Y軸上下盡頭拉到X軸最右邊所形成

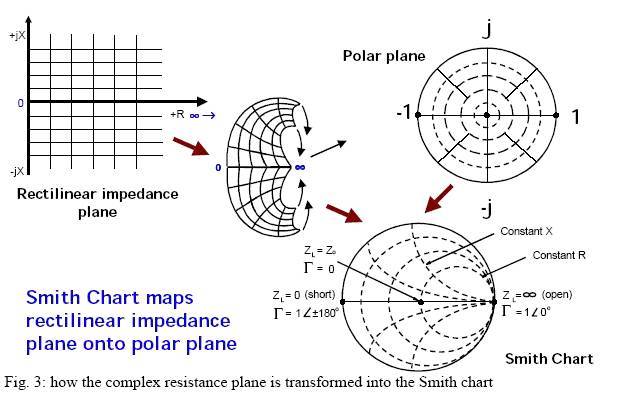
?水平軸表示實數(shù)R，水平軸以上平面表示電感性，水平軸以下平面表示電容性

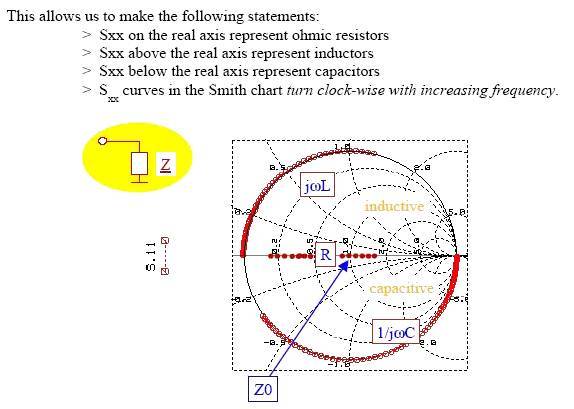
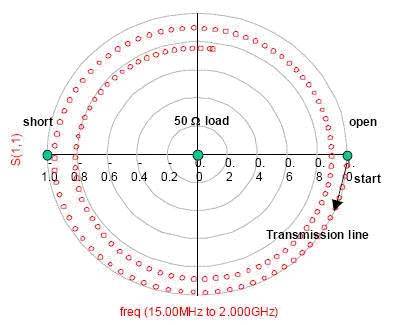
?以一條四英寸長，50歐姆的傳輸線為例，從15M~2GHz的史密斯圖，S11會呈現(xiàn)螺旋狀往圓心收斂，而這螺旋就是dielectric losses absorb造成，越高頻loss越大。

?本文目錄 下：

1. 簡介：從時域與頻域評估傳輸線特性

2. 看一條線的特性：S11、S21

3. 看兩條線的相互關系：S31、S41

4. 看不同模式的訊號成份：SDD、SCC、SCD、SDC

5. 以史密斯圖觀察S參數(shù)

6. 仿真范例 -- 地回路有沒有slot對S11, S21的影響 -- 有效介電系數(shù)如何取得

7. 問題與討論

8. Reference

6、仿真范例

取一條100mm長，線寬7mils、銅厚0.7mils、堆棧高4mils，特性阻抗50奧姆的microstrip，以下方reference plane是否有被slot切開做比對。Trace1的地回路是完整的，而Trace2的地有一個橫切的slot造成地回路不連續(xù)。

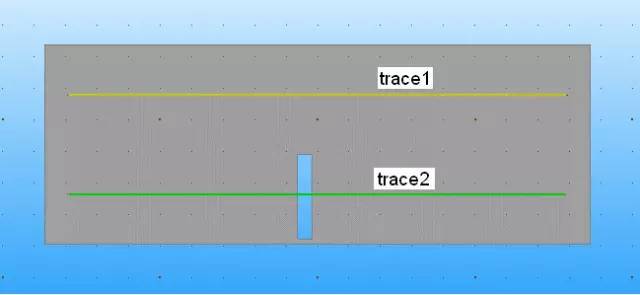
?6.1

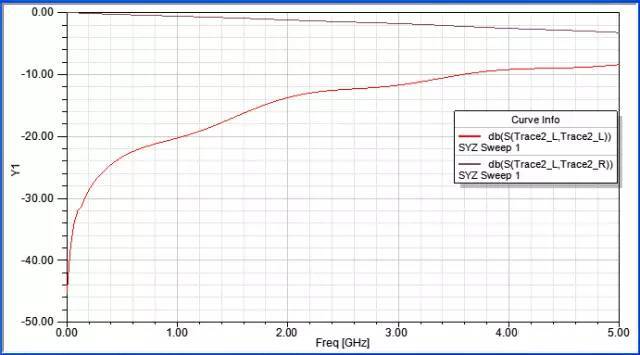
觀察Trace 1的S11、S21：S11從1~5GHz都維持在-35dB以下，表示反射成份很小；S21從1~5GHz都很接近0dB，表示大部分的訊號成份都完整的從port 1傳到port 2。

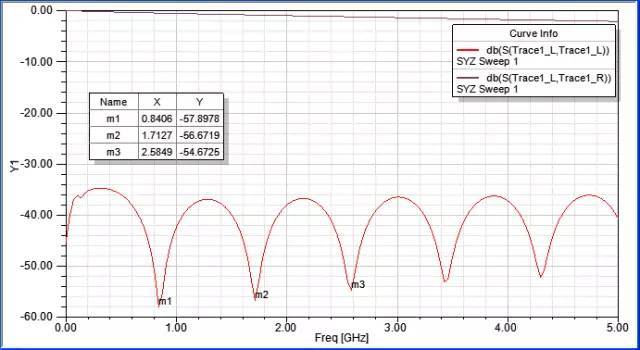
?一條良好的傳輸線，S11、S21會拉蠻開的，隨著頻率增加彼此才會慢慢靠近一些 。另外，從S11可以很清楚看到由線長所決定的共振頻點.

對于100mm長的microstrip，因為傳輸線所發(fā)射出的電力線路徑，部分是通過空氣而不是只有FR4，所以在計算諧振頻點時，介電系數(shù)若 單以4.2~4.4計算， 而不是[有效介電系數(shù)]3.085，那算出的共振頻點與模擬值會有很大誤差。

波在真空的傳遞速度等于光速：

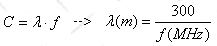
?訊號在微帶線(microstrip on FR-4)的傳遞速度：

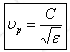
?，其中e是有效介電系數(shù)，而不是FR4的介電系數(shù)

所以，于FR4上100mm長的microstrip line，共振頻率的傳播速度 ：

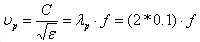
?if using e=4.3, then

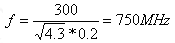
?and this result is incorrect.

if replacing e with 3.085, then

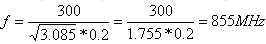
?and the value is very close to the simulation result 840MHz.

一般50歐姆特性阻抗的microstrip on FR4，有效介電限數(shù)大約3.0~3.1，可以透過Design/Nexxim得到.

6.2

觀察Trace 2的S11、S21：S11在1GHz以上時，就超過-20dB了，表示反射成份很大；S21與Trace1比較起來，隨頻率降低的速度也大一倍，表示有較多訊號成份在port 1傳到port 2的過程中損耗。

?7. 問題與討論

7.1 埠端阻抗是如何影響S11參數(shù)的?

Ans：端口阻抗(referenced impedance, Zport)會影響Zin，進而影響S11

For the transmission line with characteristic impedance Zo, the max. impedance referenced to Zport is Zin=Zo*2/Zport ，S11=(Zin-Zport)/(Zin+Zport)

在HFSS內(nèi)，上式S11中的Zport以實數(shù)考慮(non-conjugate matched load for S-parameter)，而在Designer或一般電路仿真軟件中，上式S11中的Zport以復數(shù) 考慮(conjugate matched load for S-parameter)。在 一些天線或waveguide的應用中，如果埠 端阻抗含虛部，而又希望可以在Designer內(nèi)看到跟HFSS的S參數(shù) 同樣結(jié)果，可從以下設定[Tools] \ [Options] \ [Circuit Options]，un-check [Use circuit S-parameter definition]。

請注意：這只是S參數(shù)埠端定義的不同，結(jié)果 都是對的，所以不管哪一種定義下，如果轉(zhuǎn)到Y(jié)或Z參數(shù)(或是從Designer透過dynamic link HFSS)去看，其值是一樣的。

?7.2 Touchstone file (.snp)跟S-parameter是什么關系?

Ans：Touchstone file (.snp)是基于每個頻點的S參數(shù)，所定義的一種頻域模型，其格式如下所示：

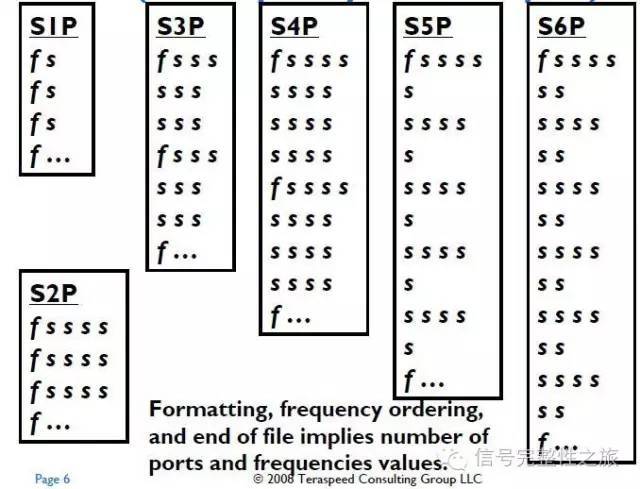
?7.3 為何端口阻抗會影響S參數(shù)，但不影響Z參數(shù)(Z11)?

Ans：Z11=Vi/Iin與埠端阻抗無關。

7.4 除了靠軟件，還有其他方法檢查Passivity、Causality嗎?

Ans：如圖所示，透過觀察TDR\NEXT\FEXT是否在T=0之前有響應。

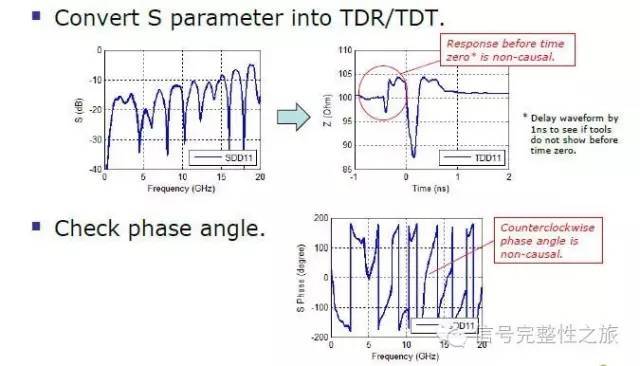
7.5 史密斯圖(Smith Chart)與Causality、Passivity是否有關聯(lián)性?

Ans：有的

7.5.1 滿足Causality與Passivity傳輸線的史密斯圖，會呈現(xiàn)以順時針方向往中心螺旋收斂的曲線。

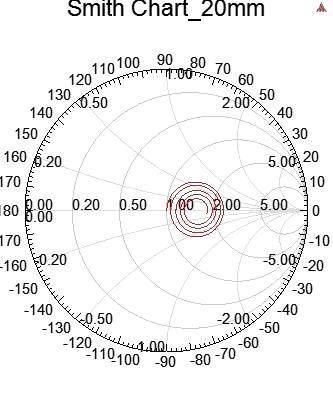
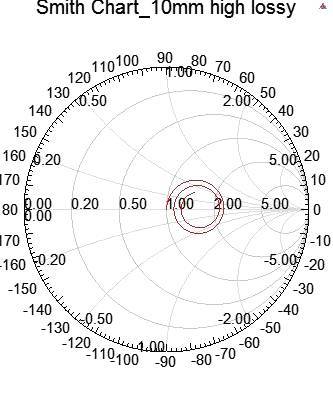
將線長從10mm拉長一倍到20mm，發(fā)現(xiàn)越長的線，其Smith Chart中隨頻率增加而順時針向中心旋轉(zhuǎn)收斂的步幅也會增加。

把介質(zhì)loss tangent從0.02改0.06，發(fā)現(xiàn)Smith Chart中隨頻率增加而順時針向中心旋轉(zhuǎn)的收斂會加快。順時針向中心旋轉(zhuǎn)與lossy有關。

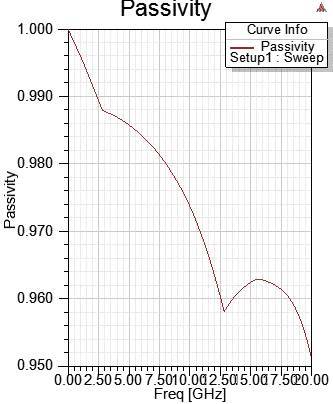
7.5.2 滿足Causality但a bit violate Passivity傳輸線的史密斯圖，會出現(xiàn)部份頻段貼合，沒有往中心 旋轉(zhuǎn)收斂。

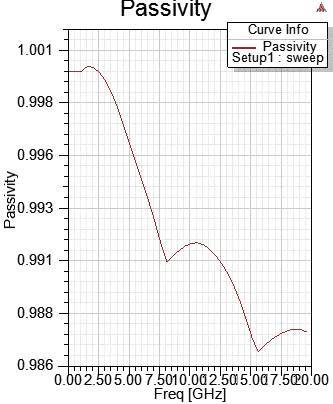
近幾年的HFSS性能一直提升，想要用簡單的例子搞出non-passivity還不太容易。本例是四條傳輸線(.s8p)，故意 降低mesh performance(放大error percentage=0.1%)，低頻DC~0.1GHz刻意不求解，并且使用lossless介質(zhì)。

7.5.3 non-causality and non-passivity的史密斯圖，相對于n*n matrix中不同矩陣區(qū)塊內(nèi)的violate程度，曲線可能會折彎 (低頻violate passivity嚴重，在Smith Chart也看到低頻曲線有不規(guī)則的折彎)，或是不往中心收斂

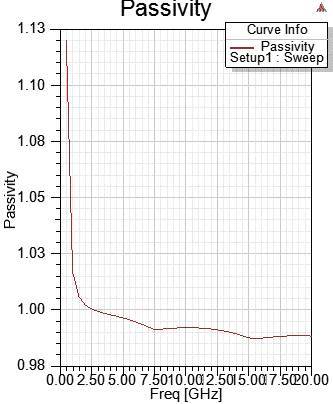
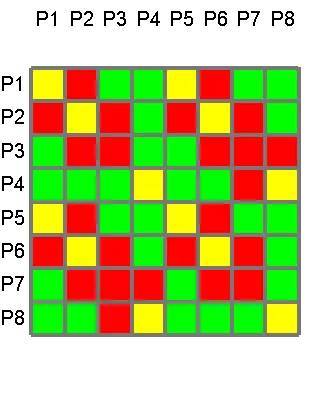
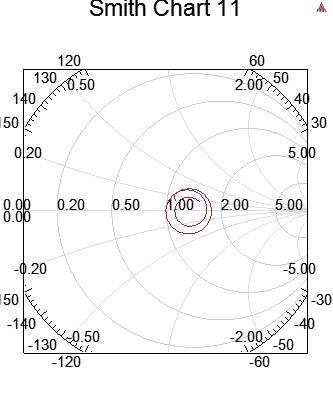
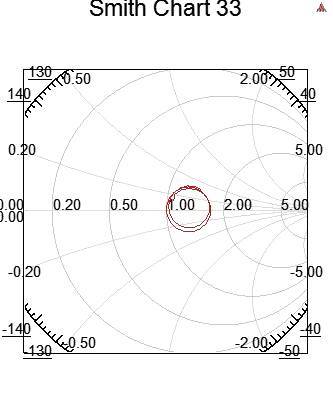
筆者還看不到HFSS產(chǎn)生的non-causal S參數(shù)的Smith Chart會逆時針旋轉(zhuǎn)，或其時域響應提前發(fā)生的現(xiàn)象 。但可以用Designer內(nèi)的de-embedded功能產(chǎn)生逆時針旋轉(zhuǎn)的Smith Chart。

8、Reference

[1] Chapter1 -- 宜蘭大學, 邱建文教授

[2] In-Situ De-embedding (ISD) p.6~8 from AtaiTec Corp. (推薦)

[3] Power Integrity for I/O Interfaces: With Signal Integrity/ Power Integrity

In a passive high-speed channel, the speedy way to check for causality is to examine the S-parameter Smith Chart. If the data rotate clockwise, it has positive group delay; implying it to be causal. On the other hand, if the data rotates counterclockwise, this implies it is noncausal.

[4] 一篇利用Smith Chart補償Passivity與Causality的專利技術

Smith Chart can be used to monitor the passivity and causality of networks under study. For instance, Foster's reaction theorem dictates a general motion in the clockwise direction with frequency for the parameters of an arbitrary network.

[5] touchstone spec. 2.0

[6] TS1.0 and TS2.0 (推薦)

[7] Converting S-Parameters from 50Ω to 75Ω Impedance

[8] Scattering Parameters：Concept, Theory, and Applications

[9] RF Matching Design

[10] Why have non-causality (推薦)

來源：信號完整性之旅